Raíz enésima de un número
Para comprender lo que es la raíz enésima de un número, es necesario tener en claro los términos de la radicación, estos son el radicando, el índice radical y la raíz:
• El radicando es el número al cual queremos hallar su raíz.
• El índice radical nos indica cuantas veces debemos multiplicar por si mismo un número para así obtener el radicando.
• La raíz es aquel número que si se multiplica por si mismo las veces que indica el índice radical, da como resultado el radicando.
Sea,
![]()
Se define a la raíz enésima de a y como el número real positivo es b se señalará que:
![]()
Se verifica entonces la siguiente igualdad:
![]()
Teóricamente tenemos que:
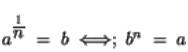
Veamos ahora algunos casos de raíz enésima
Antes de adentrarnos en los casos específicos, es importante entender que la radicación es una operación inversa a la potenciación. En la potenciación, se multiplica un número por sí mismo un cierto número de veces, mientras que en la radicación, se busca el número que, elevado a un cierto exponente, da como resultado el radicando.
1- Índice par y radicación positivo:
La radicación de un número positivo con un índice radical natural par posee dos resultados con el mismo valor absoluto, pero uno de estos valores es positivo y el otro es negativo. Veamos un ejemplo:
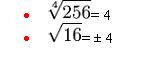
2- Índice par y radicando negativo:
No hay ningún número real que su cuadrado de como resultado un número negativo. Esto solo es posible con las unidades imaginarias (cuyos cuadrados son negativo) Un radicando negativo no tiene raíz si su índice radical es par.
Un producto de factores positivos (tanto si la cantidad es par o impar) resulta siempre en un número positivo y una serie par de factores negativos da par. Un radicando negativo con índice radical par no tendrá raíz.
Ejemplo:
![]()
Esto se cumple de tal forma ya que si fuera (+4) daría (+4)x(+4)=(+16) y si fuera (-4)x(-4)=(+16) y nunca daría como resultado (-16)
3- Índice impar y radicando positivo:
La radicación de un número positivo con índice radical natural impar posee solo una raíz positiva. Una serie de factores positivos que se multiplican por si mismos, resultan en un número positivo, tanto si la cantidad de factores son pares o impares. Entonces,
![]()
Si se tiene un producto de factores negativos, cada producto de dos factores dará un total con signo positivo. Esto no se cumple si la cantidad de factores es impar y el total será negativo.
Sea un número natural impar I y la raiz,
![]()
donde se tendrá que +R=CxCxC…etc I veces y según lo que hemos enunciado anteriormente, C debe ser positivo y no negativo para dar +R.
Ejemplos:
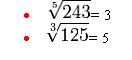
4- Índice impar y radicando negativo:
El resultado será un real negativo. La raíz de un radicando negativo, con índice radical impar, es negativa. Si multiplicamos una cantidad par de veces un número cualquiera (-A), obtenemos un total positivo (+T) y si ese total (+T) se multiplica una vez mas por (-A), el número de factores va a ser impar, con un resultante (+T)x(-A)=+Total, como explica la regla de signos de los enteros.
Ejemplo:
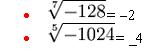
Además de estos casos, es importante mencionar que la raíz enésima de un número también puede ser calculada mediante el uso de logaritmos. El logaritmo de un número es el exponente al cual otro número fijo, la base, debe ser elevado para producir ese número. De esta manera, la raíz enésima de un número puede ser calculada como el exponente que resulta de dividir el logaritmo del radicando entre el índice radical.
Por último, es importante destacar que la raíz enésima de un número tiene aplicaciones en diversas áreas de la matemática y de la ciencia en general. Por ejemplo, en geometría, la raíz cuadrada se utiliza para calcular la longitud de la hipotenusa en un triángulo rectángulo. En física, la raíz cuadrada se utiliza en las fórmulas para calcular la velocidad y la aceleración. En estadística, la raíz cuadrada se utiliza en el cálculo de la desviación estándar, que es una medida de la dispersión de un conjunto de datos.
