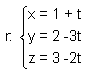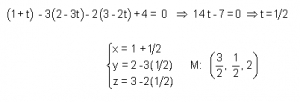Punto simétrico

Hoy continuamos con un nuevo concepto geométrico: el punto simétrico. Vamos a calcular cómo hallar el punto simétrico respecto a las diferentes variedades afines: otro punto, un plano y una recta. Pero antes de adentrarnos en los cálculos, es importante entender qué es un punto simétrico y por qué es relevante en la geometría.

La simetría es una propiedad fundamental en matemáticas y en la naturaleza. En geometría, la simetría implica que una figura o un objeto puede ser dividido o girado de tal manera que las partes resultantes sean idénticas o correspondan punto por punto. Un punto simétrico, por lo tanto, es un punto que se encuentra en la misma posición relativa respecto a un punto central, un plano o una recta, pero en el lado opuesto.

PUNTO SIMÉTRICO RESPECTO DE UN PUNTO

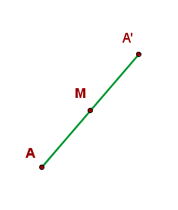
El punto simétrico A» de un punto A respecto de otro punto M, será el punto tal que la distancia del punto A al punto M es igual a la distancia del punto A» al M, es decir, d (A,M)= d (A»,M). Por tanto, podemos decir que el punto M es el punto medio del segmento AA».

Ejemplo: Hallar el punto simétrico de A(2,3) respecto al punto (-1,2).

Tenemos que hallar el punto A» tal que el punto M(-1,2) sea el punto medio de AA».

Recordemos que para calcular el punto medio entre dos puntos P(a,b) y P»(a»,b») utilizamos la siguiente fórmula: M=(a+a»/2, b+b»/2), por tanto tenemos la siguiente igualdad: (-1,2)=(2+a»/2, 3+b»/2).

Igualando coordenada a coordenada hallamos el valor de a» y el valor de b», las coordenadas de nuestro punto:

-1= (2+a»)/2 → -2=2+a» → a»=-4

2 = (3+b»)/2 →4 = 3+b»→b»=1

Por tanto el punto de simétrico que nos piden es el punto A»(-4,1).

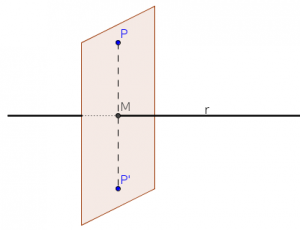
PUNTO SIMÉTRICO RESPECTO UN PLANO

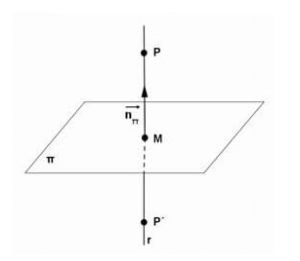
El punto simétrico P» de un punto P respecto a un plano π es el punto situado en la recta perpendicular al plano que pasa por P, tal que la distancia del punto P al plano es la misma que la distancia del punto A» al plano: d ( π ,P)= d ( π ,P»).

Para hallar el punto simétrico respecto al plano procederemos de la siguiente manera:

1º) Hallamos la recta perpendicular r perpendicular al plano que pasa por P. Por tanto, tendrá como vector director el vector normal al plano.

2º) Una vez hallada la ecuación de la recta, calculamos el punto de intersección entre el plano dado y la recta obtenida en el primer paso. Este punto será M.

3º) Por último, procedemos igual que en el primer caso, cuando se trataba de buscar el simétrico de un punto respecto del punto M.

Ejemplo: Hallar el punto simétrico del punto P(-1,3,4) respecto al plano π: x-3y-2z+4=0.

Siguiendo los pasos que acabamos de decir:

1º. Hallamos r que pasa por el punto P y tiene como vector director v=(1,-3,-2):

2º. Hallamos el punto de intersección entre el plano y la recta. Para ellos sustituimos el valor de x, y, y z en la ecuación del plano, obteniendo el valor de t. Por último, sustituimos el valor de t en las ecuaciones paramétricas de la recta y obtenemos las coordenadas del punto M:

3º. Procediendo como en el ejemplo anterior tenemos que: (3/2, ½,2)=(-1+a»/2, 3+b»/2,4+c»/2)

3/2=(-1+a»)/2 → 3=-1+a»→a»=4

1/2=(3+b»)/2 → 1=3+b»→ b»=-2

2=(4+c»)/2 → 4=4+c» →c»=0.

El punto simétrico P»(4,-2,0)

PUNTO SIMÉTRICO RESPECTO UNA RECTA

El punto simétrico P» de un punto P respecto a una recta r, es el punto que se encuentra situado en la recta perpendicular a r que pasa por P, tal que la distancia del punto P a la recta es igual a la distancia del punto P» a la recta, es decir: d(P,r)=d(P»,r).

Para hallar el punto simétrico respecto a una recta seguimos los siguientes pasos:

1º) Hallamos el plano perpendicular a r que contiene a P, para hacerlo utilizamos el vector director de la recta, que será el vector normal del plano.

2º) Hallamos el punto de corte de la recta y el plano calculado en el paso anterior, M.

3º) Por último, repetimos el mismo paso que en el caso anterior.

Ejemplo: Hallar el punto simétrico del punto P(1,2,3) respecto a la recta r: x=y=z.

Siguiendo los pasos que acabamos de decir:

1º. Hallamos el plano que es perpendicular a r y pasa por P. La ecuación del plano será x-y+z-2=0.

2º. Hallamos el punto de intersección entre la recta y el plano. Para ello, sustituimos el valor de x, y, y z en la ecuación del plano, obteniendo el valor de t. Por último, sustituimos el valor de t en las ecuaciones paramétricas de la recta y obtenemos las coordenadas del punto M: M(2,2,2).

3º. Procediendo como en los ejemplos anteriores tenemos que: (2,2,2)=(1+a»/2, 2+b»/2,3+c»/2)

2=(1+a»)/2 → 4=1+a»→a»=3

2=(2+b»)/2 → 4=2+b»→ b»=2

2=(3+c»)/2 → 4=3+c» →c»=1.

El punto simétrico P»(3,2,1)

Como hemos visto, el cálculo de puntos simétricos es una herramienta muy útil en geometría. Nos permite entender mejor la estructura de las figuras y objetos, y nos proporciona una forma de describir y analizar su simetría. Aunque los cálculos pueden ser complejos, con práctica y comprensión de los conceptos subyacentes, se pueden realizar con éxito.