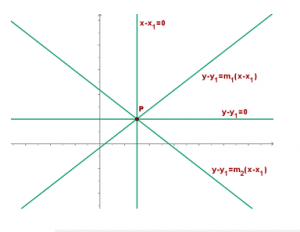
Haz de rectas

Vamos a dedicar unos días a tratar aspectos geométricos que todavía no se han tratado. Hoy vamos a ver un nuevo concepto: haz de rectas.

HAZ DE RECTAS EN EL PLANO

Definición: Llamamos haz de rectas al conjunto de rectas del plano que pasan por un punto, este punto se denomina vértice.

La ecuación del haz de rectas que pasa por el punto P(x1, y1) es: y–y1 = m (x-x1), dándole a m los distintos valores obtenemos la rectas del plano que forman el haz.

Esta ecuación también se puede escribir de la siguiente manera: α(x-x1)+β(y-y1) = 0.

Ejemplo: a) Hallar el haz de rectas que pasa por el punto P (2, -1).

b) De entre todas las rectas del haz, determina la que pasa por el origen.

a) Sustituyendo en la ecuación del haz tenemos que: α(x-2)+β(y+1) = 0.

b) Para hallar la recta exacta que pasa por ese punto, sustituimos en la ecuación anterior (x,y)=(0,0) para hallar el valor de α y β: α(0-2)+β(0+1) = 0 → -2 α + β=0 → β= 2 α.

Sustituyendo en la ecuación que hemos obtenido en el apartado a, tenemos: α(x-2)+2α (y+1) = 0 → x-2+2y+2=0 → x+2y=0

HAZ DE RECTAS DADO POR DOS RECTAS

Dadas dos rectas en el plano, r: Ax+By+C=0 y s: A»x+B»y+C»=0, definimos el haz de rectas por la siguiente ecuación: α(Ax+By+C)+ β(A»x+B»y+C») = 0. Dándole valores a α y β obtenemos las rectas que pasan por el punto donde se cortan las dos rectas. Al punto de intersección se le denomina vértice.

Ejemplo: a) Escribe la ecuación del haz formado por las rectas: r: 3x-y+2=0 y s: x-y+4=0.

b) Halla el vértice del haz.

c) Calcula la recta del haz que pasa por el punto A(-1,2).

a) Sustituyendo en la ecuación que hemos visto: α(3x-y+2)+ β(x-y+4) = 0

b) Para hallar el vértice, resolvemos el sistema que forman las dos ecuaciones de la recta, obteniendo el punto P(1,5).

c) Por último, para hallar la recta que pasa por el punto A, sustituimos en la ecuación del haz obtenida en el apartado a): c) α(3∙(-1)-2+2)+ β(-1-2+4) = 0 → -3 α+β=0 → β= 3 α.

Siguiendo el mismo procedimiento que en el ejemplo anterior, tenemos: α(3x-y+2)+ 3α (x-y+4) = 0 → 3x-y+3+3x-3y+12=0 → 6x-4y+15=0.

HAZ DE RECTAS PARALELAS

El haz de rectas paralelas dadas a la recta r: Ax+By+C=0 es el conjunto de todas las rectas que son paralelas a la recta r. El haz de rectas viene determinado por la ecuación: Ax+By+k=0, de tal forma que dándole distintos valores a k obtenemos las diferentes rectas paralelas.

Ejemplo: Hallar la ecuación del haz de rectas paralelas a la recta t: -x/2+y/3=2.

En primer lugar vamos a pasar la ecuación a forma general: -3x+2y=12. Una vez que ya tenemos la recta en forma general, sustituimos en la ecuación dicha anteriormente, por tanto la ecuación del haz de rectas paralelas a t es: -3x+2y+k= 0.

De forma análoga al haz de rectas, también se puede definir el haz de planos en el espacio, que determinará la recta donde cortan.