Punto de contacto

Se llama punto de contacto o tangencia al punto en común entre una circunferencia y la tangente. En geometría la recta tangente es aquella que posee un punto en común con una curva. Una recta y una circunferencia pueden tener dos puntos, un solo punto o ningún punto en común. Veamos estos casos en la siguiente representación:

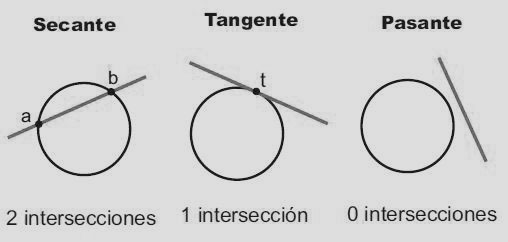
El punto de intersección es el punto de contacto o el punto de tangencia, como podemos ver es una línea que intercepta al círculo en un punto.

Dadas una circunferencia alrededor de O y una recta t, con un punto de tangencia P y si el radio OP de la circunferencia es perpendicular a la recta t. Diremos entonces que t es tangente a la circunferencia en el punto P. Si demostramos esto podemos decir que una recta t y una circunferencia con el centro en O tienen a P como punto de tangencia o contacto Y OP será perpendicular a t, por lo cual se cumple lo siguiente. Según la rotación del radio OP, t y la circunferencia se cambian de posición entre ellas. Si la circunferencia y la recta t tuvieran un punto de tangencia Q su punto de imagen Q ‘ tendría que encontrarse sobre la circunferencia y sobre la recta t. Por lo tanto la circunferencia y la recta t tendrían tres puntos en común que serían P, Q Y Q’ . Pero este hecho no es posible, por lo que P será el único punto de contacto y t la tangente. Veamos el siguiente ejemplo:

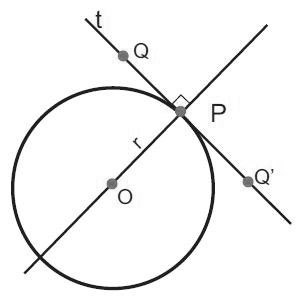
Ahora veamos la proposición inversa de lo dicho anteriormente, o sea un nuevo teorema con el cual podremos verificar si una recta es tangente a una circunferencia.

Si tenemos una circunferencia alrededor de O y una recta t, con un punto de tangencia o de contacto P, la recta t será una tangente a la circunferencia y el radio OP será perpendicular a la recta t. Si la recta t y la circunferencia tienen a P como punto de contacto se cumplirá lo siguiente. Si se manifiesta la circunferencia con centro O y una radio r respecto a la tangente t, se consigue una nueva circunferencia con centro O’. La imagen de P es el mismo y el único punto de tangencia de t y de ambas circunferencias. Estas circunferencias tienen el mismo radio. El segmento O O’ debe pasar por P. De esta forma OP es parte de OO’, que será un segmento que manifestará y reflejará O a O’ y será perpendicular al eje t. Entonces concluiremos en que OP Y t son perpendiculares. Veamos entonces una representación de esto:

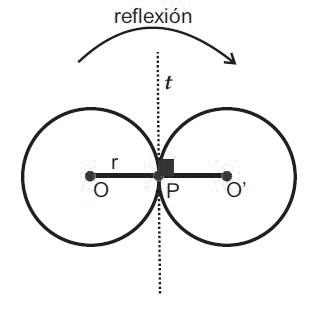
Además de los conceptos básicos, es importante entender algunas propiedades y teoremas relacionados con los puntos de tangencia.

Por ejemplo, si dos circunferencias son tangentes en un punto, entonces el segmento de línea que une sus centros pasa por el punto de tangencia. Esto se conoce como el teorema de las circunferencias tangentes. Este teorema es útil en muchos problemas de geometría y puede ayudar a simplificar los cálculos.

Otra propiedad interesante es que si una recta es tangente a una circunferencia, entonces la distancia desde el centro de la circunferencia hasta la recta es igual al radio de la circunferencia. Esta propiedad es útil para encontrar la ecuación de la recta tangente a una circunferencia en un punto dado.

Además, si una recta es tangente a una circunferencia en un punto, entonces la recta es perpendicular al radio de la circunferencia en ese punto. Esta propiedad es útil para probar que una recta es tangente a una circunferencia.

Por último, es importante mencionar que el concepto de punto de tangencia no se limita a las circunferencias y las rectas. También puede aplicarse a otras curvas, como las elipses, las parábolas y las hipérbolas. En estos casos, la definición y las propiedades del punto de tangencia pueden variar ligeramente, pero el concepto básico sigue siendo el mismo: un punto de tangencia es un punto en el que una recta toca a una curva sin cruzarla.