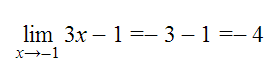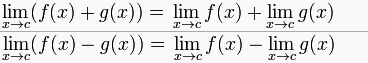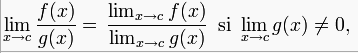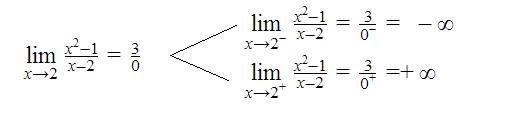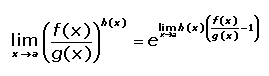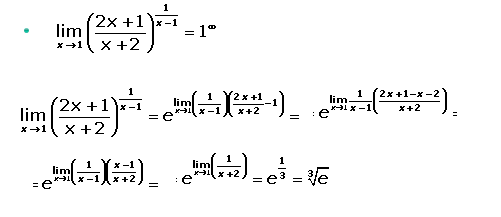Límite en un punto

Después de una larga semanita estudiando conceptos geométricos, vamos a cambiar de campo, hoy nos toca conceptos del análisis, además un concepto que ya conocemos, pero sobre el que no hemos profundizado. El límite de una función en un punto y como resolver cada caso, así como recordar algunas de sus aplicaciones.

DEFINICIÓN

En primer lugar vamos a estudiar la definición formal de límite (usada sobre todo en demostraciones), y a continuación, veremos la definición que utilizaremos de forma práctica en la resolución de ejercicios.

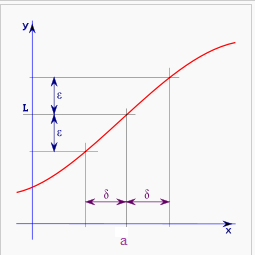
Definición: Diremos que el límite de la función f(x) es L, es decir, f(x) se acerca al valor L cuando x se aproxima al valor a, si y sólo si para todo ε>0, existe un valor δ>0 tal que si |x- a|< δ, entonces |f(x)-L|< ε.

En la siguiente imagen podemos visualizar el concepto que acabamos de definir:

Definición: El límite de una función f(x) en el punto a, es el valor que se obtiene cuando sustituimos el valor de x=a en la función:

Ejemplo: Calcula el límite de la función f(x)=3x-1 cuando x→ -1.

Nota: Pero no siempre calcular el límite es tan fácil, hay algunas funciones que al sustituir no nos da un valor en concreto y tenemos que realizar una serie de cálculos para poder obtener el valor. Estos casos especiales son los conocemos como indeterminaciones.

PROPIEDADES DEL LÍMITE DE UNA FUNCIÓN EN UN PUNTO

Dadas f(x) y g(x) dos funciones, se cumple:

1. El límite de una suma o resta es igual a la suma o resta de los límites.

2. El límite de un cociente es igual al cociente de los límites.

3. El límite de un producto es igual al producto de los límites.

4. El límite de una potencia:

5. Una de las propiedades más importantes es la que utilizamos para resolver indeterminaciones con potencias:

INDETERMINACIONES

Como ya hemos comentado en la nota del primer apartado, cuando resolvemos un límite aplicando las propiedades nos podemos encontrar con situaciones especiales: las indeterminaciones. Nos encontramos 3 tipos distintos:

Tipo 1: Indeterminación 0/0.

En este tipo de indeterminación nos podemos encontrar dos casos distintos:

-Caso a) Que resolveremos factorizando, ya sea por Ruffini o sacando factor común. Una vez que simplificamos, volvemos a sustituir por el valor de x:

-Caso b) Cuando en la función hay raíces cuadradas, tenemos que multiplicar numerador y denominador por el conjugado. Operamos teniendo en cuenta que suma por diferencia es diferencia de cuadrados, desapareciendo la raíz en el numerador o denominador. A continuación, si volvemos a obtener la indeterminación 0/0, volvemos al caso a) y tenemos que factorizar y simplificar:

Tipo 2: Indeterminación k/0.

Aunque este tipo no es exactamente una indeterminación, pero se considera un caso especial, ya que aunque siempre que tenemos k/0=∞, tenemos que realizar los límites laterales para determinar el signo del infinito. Este tipo de límites es el que nos aparece siempre que estudiamos las asíntotas verticales.

Tipo 3: Indeterminación 1 elevado a ∞.

Teniendo en cuenta la propiedad número 5, este límite se puede resolver haciendo transformaciones para llegar a una expresión similar, o utilizando la siguiente fórmula:

Vamos a resolver el siguiente ejemplo utilizando únicamente la fórmula: