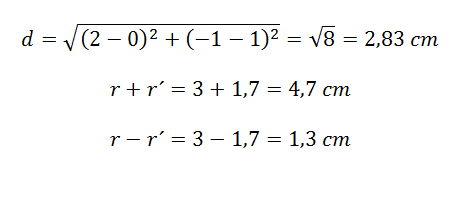Geometría de la circunferencia
Ya en anteriores ocasiones hemos estudiado algunas de las características de la circunferencia, como son los puntos de contacto, es decir la posición relativa de una circunferencia y una recta. Pero ahora ha llegado el momento de estudiar más cosas sobre la geometría de la circunferencia. Para empezar veremos unas definiciones formales previas:
DEFINICIONES
Llamamos circunferencia de centro O y radio r al conjunto de los puntos del plano que equidistan del punto O una distancia igual al segmento r.
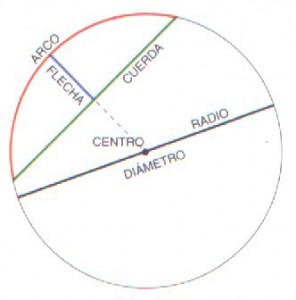
Llamamos radio de la circunferencia al segmento que une cualquier punto A de la circunferencia con el centro O.
Llamamos diámetro de la circunferencia al segmento que une cualesquiera dos puntos de la circunferencia A y A´ pasando por el centro O.
Llamamos cuerda al segmento que une dos puntos cualesquiera de la circunferencia.
Llamamos arco de la circunferencia al segmento de circunferencia que une dos puntos.
Se llama círculo a todos los puntos cuya distancia a O es menor que r. Estos puntos se denominan puntos interiores, mientras que los puntos cuya distancia es mayor que r se denominan puntos exteriores.
POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS
Sean dos circunferencia C y C´, cuyos centros y radios son O,r y O´,r´ respectivamente, llamemos d a la distancia entre O y O´, es decir, d=OO´; entonces pueden darse los siguientes casos:
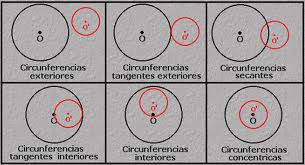
Caso 1: Circunferencias exteriores:
En este caso los puntos de C son exteriores de C´ y viceversa, los puntos de C´ son exteriores de C. Se cumple que: d>r+r´>r-r´.
Caso 2: Circunferencias tangentes exteriores:
Si las circunferencias son tangentes exteriores solo tienen un punto en común, el punto de tangencia, siendo todos los demás exteriores como en el caso anterior. Se cumple que: : d=r+r´>r-r´.
Caso 3: Circunferencias secantes:
En este caso las circunferencias tienen dos puntos en común, los puntos de corte o intersección. Se cumple que: r+r´>d>r-r´.
Caso 4: Circunferencias tangentes interiores:
Como las dos circunferencias son tangentes, tienen un punto en común, como en el caso 2, que llamamos punto de tangencia. Pero en este caso, por ejemplo considerando que C´ es interior a C, todos los puntos de C´ son puntos interiores de la circunferencia C. Se cumple que: r+r´>r-r´=d.
Caso 5: Circunferencias interiores:
Si consideramos que C´ es interior al a circunferencia C, entonces todos los puntos de C´ son puntos interiores de C. Se cumple que : r+r´>r-r´>d
Caso 6: Circunferencia concéntricas:
Por último, diremos que C y C´ son circunferencias concéntricas cuando ambas tienen el mismo centro, O=O´, por tanto d=0. Además todos los puntos de C´ son interiores de C.
En la siguiente imagen podemos visualizar todos los casos anteriores facilitándonos de esta manera la comprensión de lo anteriormente visto.
Para finalizar por hoy, vamos a ver un problema de posiciones relativas de circunferencias:
Ejemplo: Estudiar la posición relativa de dos circunferencias sabiendo que el radio de la primera circunferencia es de 3cm y el origen está en el punto O(0,1); mientras que el radio de la segunda es de 17dm y su centro está en el punto O´(2,-1).
En primer lugar, escribiremos los datos del problema, teniendo en cuenta que todo debe estar en las mismas unidades:
C={r=3cm, O(0,1)} y C´={r´=1,7cm y O´(2,-1)}
Hallamos el valor de d, y estudiamos la relación entre d, r+r´y r-r´. Evidentemente podemos descartar el último caso, ya que no tienen el mismo centro.
Luego se cumple que r+r´>d>r-r´, por tanto las circunferencias son secantes.