Ángulos de una circunferencia
Después de ver las posiciones relativas de dos circunferencias, hoy vamos a estudiar los ángulos de una circunferencia.
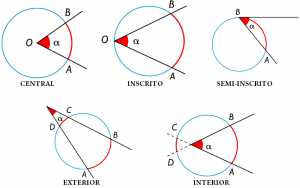
Ángulo central: Es el ángulo que tiene su vértice en el centro de la circunferencia, es decir, un ángulo determinado por dos semirrectas que tienen el origen en el centro, y por tanto son radios de la circunferencia. Los puntos correspondientes al círculo abarcados por el ángulo central se llaman sector circular correspondiente a dicho ángulo.
Diremos que dos ángulos son equivalentes cuando sus ángulos centrales correspondientes sean iguales.
Ángulo inscrito: Es el ángulo cuyo vértice se encuentra en un punto cualquiera de la circunferencia. Además los lados de un ángulo inscrito son secantes a la circunferencia. El valor del ángulo central es la mitad del ángulo inscrito que abarca el mismo arco.
Si el ángulo central es un ángulo de 180º, entonces el ángulo inscrito es un ángulo de 90º, es decir, un ángulo recto.
Ángulo semiinscrito: Es el ángulo cuyo vértice es un punto de la circunferencia y uno de sus lados es tangente a la circunferencia mientras que el otro es secante a ella. El valor de un ángulo semiinscrito es igual al del ángulo inscrito que abarca.
Ángulo exterior: Es el ángulo que tiene su vértice fuera de la circunferencia, es decir que la distancia del vértice al centro es mayor que el radio de la circunferencia; y sus lados son secantes a la circunferencia. El valor de un ángulo exterior es la semidiferencia de los arcos que abarca:
Ángulo interior: Es el ángulo cuyo vértice está en la parte interior de la circunferencia, es decir, que la distancia del vértice al centro de la circunferencia es menor que el radio. El valor de un ángulo interior es igual a la semisuma de los ángulos que comprenden él mismo y su opuesto.
A continuación podemos ver cada uno del os siguientes ángulos en la siguiente imagen:
Por último vamos a realizar el siguiente ejemplo en el que conocidos la medida de algunos de los ángulos nos piden calcular todos los demás que se muestran:
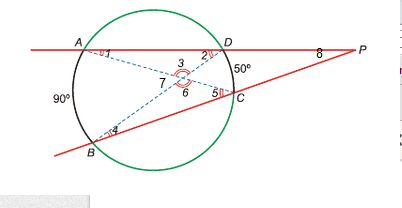
Ejemplo: Halla el valor de los ángulos indicados en la figura por número indicando el proceso seguido:
El ángulo 1 y el ángulo 4 son ángulos inscritos que abarcan un ángulo de 50º, por tanto 1=4=50/2=25º.
El ángulo 2 y el ángulo 5 son también ángulos inscritos que abarcan un ángulo de 90º, por tanto 2=5=90/2=45º.
El ángulo 3, si nos fijamos forma un triángulo con el 1 y 2, como sabemos que los ángulos de todo triángulo tienen que sumar 180º, entonces 3=180-(25+45)=110º.
El ángulo 6, al igual que el ángulo 3, forma un triángulo con el 4 y 5, por tanto 6=180-(25+45)=110º.
El ángulo 7, es un ángulo interior a la circunferencia, y por tanto tenemos que calcular la semisuma de los ángulos que abarca: 7=(90+50)/2=70º.
El ángulo 8, es un ángulo exterior a la circunferencia, por tanto para hallar su valor calculamos la semidiferencia de los arcos que abarca: 8=(90-50)/2=20º.