Proporcionalidad inversa

Hola de nuevo, en este articulo vamos a descubrir a la proporcionalidad inversa, hermana antagónica de la proporcionalidad directa.

¿Qué por qué digo lo de antagónica? Bueno, pues sencillamente porque es todo lo contrario a la anterior. Recordemos que una proporción directa se daba si la razón de la proporción era la misma, es decir, si aumentaba una cantidad, la otra aumentaba en la misma medida. Pues bien, en este caso es algo parecido:

Pensemos en cierta construcción, en la que se necesitan apilar 5000 ladrillos. Si solo hubiese un hombre, apilando ladrillos noche y día a razón de 40 ladrillos por hora (supongamos que no tiene carretilla), tardaría unas 125 horas (unos 5 días), en terminar el trabajo. Ahora imaginemos que este hombre, llama a sus vecinos para que le vengan a ayudar, al final consigue reunir a 5.

En total, si todos llevan la misma cantidad de ladrillos, cada hora apilarán 40×5= 200 ladrillos/hora. Lo que resulta en que terminarán el trabajo en 5000/200 = 25 horas (un día y una hora).

Os dejo una tabla para que lo veáis en detalle:

Se ve fácilmente que el número de horas se reduce cuanto más trabajadores se unen. Entonces, ahora estamos ante una proporción indirecta, cuyas cantidades aumentan de forma inversamente proporcional, es decir, cuando una aumenta la otra disminuye.

Otra forma de resolver el problema es mediante la razón de proporcionalidad, que en el caso de las proporciones inversas se halla multiplicando las magnitudes entre si(es decir, horas por hombres). La cantidad que obtenemos, 125, se llama constante de proporcionalidad, y como su nombre indica es constante(siempre igual), por lo que si quisiésemos saber cuántos hombres necesitaríamos para terminar la obra en 25 horas, procederíamos así: 125/25 = 5 hombres. Lo mismo para las demás magnitudes.

Un ejemplo que se da en la vida real es cuando vamos en coche/bus hacia nuestro lugar de trabajo/centro de estudios. El tiempo que tardamos en llegar depende de la velocidad a la que viajemos, pues a más velocidad, más distancia recorreremos, y por tanto, haremos el recorrido en menor tiempo. De aquí deducimos que la distancia recorrida es inversamente proporcional a la velocidad. Me voy a permitir la licencia de poneros la formula, pero ya os adelanto que esto lo veréis solamente en física:

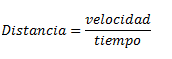
Siendo en nuestro caso D la distancia y variable constante, cuyas variables, velocidad y tiempo, modificaremos para encontrar la solución.