Proporcionalidad

Hace varios artículos atrás hablábamos de lo que es proporcional, cuando hablábamos de la semejanza de triángulos. Recordemos que básicamente nos referíamos a proporcionalidad como una relación entre medidas o magnitudes, la cual si se cumplía decíamos que esas medidas eran proporcionales.

Cuando hablamos de proporciones numéricas, decimos que existe una relación entre varios números, como puede ser a, b, c y d:

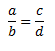
Esto se lee como a es a d, como b es a c, esta definición tiene sentido, pues si aplicamos la propiedad de las proporciones, el producto de extremos es igual al producto de medios, siendo éstos a y d (los extremos) y b y c (los medios). Se trata simplemente de multiplicar en cruz los diferentes coeficientes.

Pero veamos unos ejemplos para intentar explicar un poco esto de la proporcionalidad:

 

En un envase de cierta bebida, encontramos la cantidad necesaria de agua que se necesita para preparar el producto concentrado:

 

Ambas cantidades poseen un cociente que las relaciona, este cociente da lugar a fracciones equivalentes:

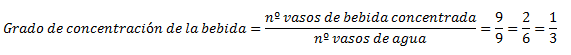
De aquí, tenemos el 1/3, que como es la única fracción que no se puede reducir y representa la proporción de los distintos elementos, pues si multiplicamos por 2 y por 3 podemos obtener las restantes fracciones.

Hay que tener en cuenta que no siempre podemos encontrar proporcionalidades entre medidas o magnitudes. Pensemos por ejemplo, en el área de un cuadrado, que como sabemos, es lado por lado, lado al cuadrado.

Si el lado es 2, su área vale 4, pero sin embargo, si cogemos otro cuadrado con tres veces más lado que el anterior, su área no se triplica, pues teniendo 6 cm de lado, el área sería 6×6=36, por tanto, no nos da el doble que la anterior, que sería 12.

En resumen, la proporcionalidad, cuando se cumple, se refiere a que esas medidas cumplen una determinada relación, que se puede extraer, y que se da siempre sin excepción. Dicha relación es la base para hallar las famosas reglas de tres, que veremos más adelante.