Identidad de Euler

Leonhard Paul Euler fue un importante matemático y físico nacido en Basilea el 15 de abril del año 1707. Se le considera Es considerado uno de los matemáticos mas influyentes y prestigiosos del siglo XVIII. Se denomina identidad de Euler a una fórmula que fué desarrollada por este matemático, como ya nos dice el nombre de la identidad.

Esta fórmula no solo es una simple ecuación, sino que es una representación de la belleza y la elegancia de las matemáticas. La identidad de Euler es una ecuación que combina cinco de los números más importantes en matemáticas: 0, 1, e, i y π. Estos cinco números son fundamentales en muchos campos de las matemáticas y la física, y la identidad de Euler los une en una sola ecuación, lo que es una hazaña impresionante.

Se puede observar en ella como va evolucionando el concepto numérico a través de los años. Desde la concepción más instintiva, como la de los naturales (que ya se conocen desde la época prehistórica) hasta los números negativos (representados por -1) obteniendo luego los números enteros. Si se agregan las fracciones (no figuran) se obtiene como resultado a los números racionales. Después, añadiendo los irracionales (e y π) se obtienen los reales. Como punto final si se agregan los imaginarios imaginarios (se representan por i) obtenemos finalmente a los números complejos.

También se puede observar en esta identidad la historia de la evolución matemática, en este caso de las operaciones aritméticas. Podemos ver una suma, un producto y también una potencia. Esta identidad es interesante y valiosa , ya que relaciona cinco números muy utilizados en matemáticas:

• e (número de Euler o constante de Napier) esencial en análisis. Este es un número irracional muy popular y también es uno de los números más trascendentes en matemáticas. Sus primeras cifras son las siguientes, 2,71828182845904523536028747135 ( continúa…)

• π (pi) es un número esencial en geometría (corresponde a la relación entre la longitud de una circunferencia y su diámetro, pi = 3,14159265)

• i (imaginario) es un número de gran importancia algebraica. Un número imaginario es un número que tiene como cuadrado a un negativo

• 0 y 1 Son las bases aritméticas puesto que son los elementos neutrales correspondientes a la adición y a la multiplicación

Estos números no parecían guardar gran relación entre ellos. Pero Euler descubrió su relación, hecho que sorprendió al mundo de las matemáticas. Veamos entonces la identidad que relaciona a estos números:

O escrito de otro modo:

Entonces ¿Por qué razón decimos que hay una igualdad? Veamos:

Se Parte de una expresión correspondiente a la exponencial a modo de suma de los términos de la sucesión o serie:

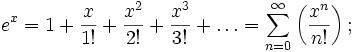
Se sustituye x por z.i, y se aplica lo que sigue,

(a raíz de esto se repite el ciclo de resultados) agrupandose las potencias por pares de z de un lado y las impares por otro lado, obteniendo de esta forma:

Si se sabe que las expresiones de sin x y cos x a modo de serie son:

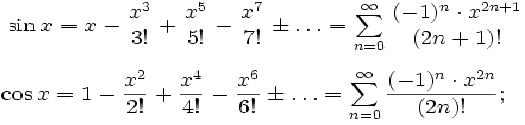
llegamos a:

Sustituímos z por π (Pi):

Pasando -1 a la izquierda como +1 llegaremos entonces a la fórmula.

La identidad de Euler es una de las ecuaciones más bellas de las matemáticas, y es una de las pocas ecuaciones que tiene su propia fiesta, el Día de Pi, que se celebra el 14 de marzo (3/14 en la notación de fecha estadounidense). La belleza de la identidad de Euler proviene de su simplicidad y de la forma en que une cinco de los números más importantes en matemáticas. La identidad de Euler es un ejemplo perfecto de cómo las matemáticas pueden ser tanto bellas como útiles.