Funciones trigonométricas
La utilización de las llamadas funciones trigonométricas data de la época de la antigua Babilonia. Los principios de esta rama matemáticas fuerón desarrollados en su mayoría por estudios de la India, antigua grecia y matemáticos musulmanes.
Las funciones trigonométricas surgen al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados dependen únicamente del valor de los ángulos del triángulo.
La denominación de los lados de un triángulo rectángulo son las siguientes:
* La hipotenusa (h) corresponde al lado que se encuentra opuesto al ángulo recto.
* El cateto opuesto (a) corresponde al lado opuesto al ángulo que se quiere establecer.
* El cateto adyacente (b) corresponde al lado que es adyacente al ángulo que se busca establecer.
Si se considerna los triángulos rectángulos ABC, rectángulos en A, tenemos que
![]()
Todos los triángulos representados con estos ángulos serán semejantes, por lo cual, las medidas de sus lados serán proporcionales:
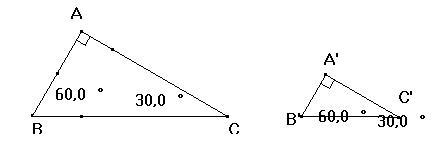
Esto quiere decir que si se procede a calcular el primer triángulo AC/BC se obtendrá como resultado el mismo que hubiera sido si calculáramos en el triángulo segundo el cociente A’C’/B’C’.
En un triángulo rectángulo se puede definir como seno de un ángulo agudo al valor que se obtiene al dividir la longitud del cateto opuesto al ángulo entre la longitud de la hipotenusa.
Definimos el coseno de un ángulo agudo como valor obtenido al dividir la longitud del cateto contiguo al ángulo entre la longitud de la hipotenusa.
Definimos como tangente de un ángulo agudo al valor del cociente que se obtiene al dividir la longitud del cateto opuesto entre la longitud del cateto contiguo.
sen(B) = AC/BC
cos(B) = BA/BC
tan(B) = AC/BA
Las razones trigonométricas son generalizadas para ángulos cualesquiera, usando una circunferencia de radio 1 y cuyo centro se ubica en el origen. Los ángulos se miden en sentido contrario a las agujas del reloj.
Además de su uso en el estudio de los triángulos, las funciones trigonométricas también son fundamentales en una variedad de otras áreas de las matemáticas, incluyendo el cálculo, la geometría y la teoría de números. En particular, son esenciales para entender las propiedades de las ondas y las oscilaciones, y desempeñan un papel clave en la física y la ingeniería.
Las funciones trigonométricas también son útiles en la resolución de problemas de la vida real. Por ejemplo, se utilizan en la navegación para determinar la distancia entre dos puntos en la Tierra, en la arquitectura para calcular la altura de los edificios, y en la astronomía para medir la distancia entre los planetas y las estrellas.
Propiedades importantes:
a)
![]()
Esta igualdad se conoce generalmente como fórmula fundamental de la trigonometría. Se demuestra de forma muy sencilla si se aplica el teorema de Pitágoras.
b)
![]()
Esta igualdad se demuestra a partir de las definiciones de seno, coseno y tangente.
c) los valores del seno y del coseno se comprenden entre -1 y 1.
Al estar definidos los senos, cosenos y tangentes para un ángulo cualquiera, se da lugar a la concepción de las funciones trigonométricas.
A continuación veremos la definición de las funciones trigonométricas:
• El seno corresponde a la relación que se encuentra entre la longitud del cateto opuesto e hipotenusa:
![]()
No es influyente el tamaño del triángulo para con el valor de la relación en cuestión siempre y cuando posean igual ángulo.
• La relación entre la longitud de la hipotenusa con la del cateto adyacente corresponde al coseno de un ángulo, veamos:
![]()
• La tangente de un ángulo corresponde a la relación entre la longitud del cateto opuesto y la del adyacente:
![]()
• La relación entre la longitud del cateto adyacente y la del cateto opuesto es lo que llamamos cotangente.
![]()
• La secante de un ángulo corresponde a la relación entre la longitud del cateto adyacente y la hipotenusa.
![]()
• La relación entre la longitud de la hipotenusa y cateto opuesto es la cosecante.
![]()
Las funciones trigonométricas son herramientas poderosas que permiten resolver una amplia gama de problemas en diversas disciplinas. Su estudio y comprensión son fundamentales para cualquier estudiante de matemáticas o ciencias.
