Propiedades de las ecuaciones

Como hemos visto antes, para que la igualdad de una ecuación se mantenga, es necesario efectuar una serie de operaciones entre sus términos, al no respetarse esto podría darse el caso que no pudiésemos encontrar la solución de dichas ecuaciones. Bien, vayamos entonces a ver cuáles son estas propiedades:

 

1º Si a una ecuación de primer grado se les suma o resta el mismo número o una ecuación semejante (con las mismas incógnitas) a las que posee la ecuación, entonces se obtiene una ecuación que es equivalente a la que teníamos. Lo mismo sucede cuando restamos. Veamos unos ejemplos:

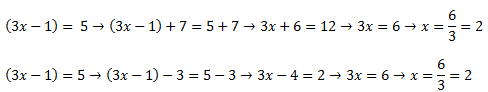
Como os daréis cuenta, hemos suma y restado en la misma ecuación dos números totalmente distintos entre si, pero la solución de la ecuación es la misma, ¿Cómo es posible? Pues aparte de lo que dice la propiedad que vimos arriba, si os fijáis, en el primer ejemplo, si tenemos dos 5 a ambos lados de la ecuación, y además con el mismo signo, si agrupásemos todos los números en un lado 5-5 no daría cero, es decir, como sumamos los mismo en los dos lados, no modificamos la ecuación.

 

2º Cuando se multiplica o se divide por un número distinto de cero, en ambos lados de la igualdad, la igualdad no varía.

Escogemos la misma ecuación de antes, y vamos a realizar una multiplicación y una división:

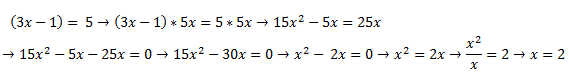
Para poder resolver esta ecuación, hemos tenido que juntar todas las equis, simplificar la ecuación sumando las equis de igual base y mismo exponente para después poner en un lado el x^2 y al otro lado los coeficientes con x de grado uno, para así conseguir despejar. Si os fijáis, 5x está en ambos lados al principio, es decir, no afecta a la ecuación, ya que estamos efectuamos la misma operación en ambos extremos de la igualdad.

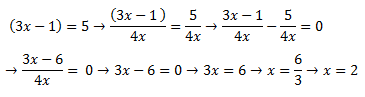
En este caso, dividimos por 4x en los dos lados de la igualdad, dando como resultado una resta de fracciones con mismo denominador, solo hemos hecho las operaciones pertinentes, para después multiplicar ese exponente en cruz por el lado derecho de la igualdad, dándonos cero, quedándonos el camino libre para despejar x. El resultado en esta ocasión no varía, ya que, al dividir en ambos lados, al igual que en la multiplicación, estamos realizando la misma operación en ambos lados, con lo cual, la solución nunca varia.

3º Si elevamos a una potencia distinta de cero ambos miembros de la igualdad, la igualdad se mantiene.

 

 

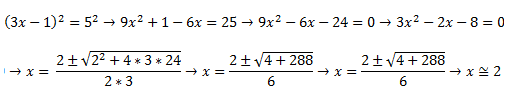
Vaya, mirad por donde nos ha salido una ecuación de segundo grado. No os preocupéis, que en el siguiente articulo os digo de donde sale esa raíz tan rara, por ahora quedaros con la idea de que, el resultado sigue siendo «el mismo» aunque hayamos elevado al cuadrado las dos igualdades. Si hacéis la cuenta, veréis que os sale dos y pico, eso es debido a la raíz cuadrada por lo cual no nos da exactamente dos, pero podemos afirmar que se acerca al mismo resultado.

 

**Pista**: Como resumen, recordad que, si hacéis lo mismo a la izquierda y a la derecha de la igualdad (restar, sumar, multiplicar, dividir o elevarlos a algo) os dará siempre lo mismo.