Ecuaciones logarítmicas

Las ecuaciones logarítmicas son aquellas ecuaciones en las que al menos una de las incógnitas es un logaritmo. Podemos expresarlo de forma general así:

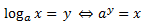
Siendo a la base del logaritmo, x una potencia cualquiera e y el resultado de ese logaritmo.

Para poder resolver estas ecuaciones debemos recordar las propiedades de los logaritmos (suma, resta, división ,multiplicación, etc.). Además, es importante tener en cuenta que los logaritmos son una herramienta matemática que nos permite simplificar y resolver ecuaciones que de otra manera serían muy difíciles de manejar. Los logaritmos son especialmente útiles en situaciones donde las variables están multiplicándose o dividiéndose a diferentes potencias.

Veámoslas con ejemplos así hacemos dos cosas al mismo tiempo:

Ejemplo 1:

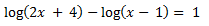
Como es una resta de logaritmos, podemos expresarlo también como el logaritmo de la división de lo que hay entre paréntesis:

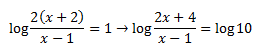
El log10 sale de sustituir el 1 de la derecha, ya que el logaritmo en base 10 de log10 es efectivamente, 1. Eliminamos pues los logaritmos de ambos lados, quedándonos:

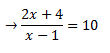
Simplificamos:

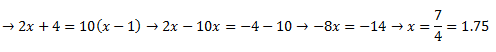
Ya veis que la ecuación logarítmica solo dura una línea, todo lo demás es una ecuación normal. Pero no olvidemos que el logaritmo es una operación inversa a la exponenciación, por lo que puede ser útil pensar en una ecuación logarítmica en términos de exponenciación. Por ejemplo, la ecuación logb(x) = y es equivalente a la ecuación b^y = x.

Ejemplo 2:

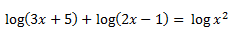
Se nos presenta entonces una ecuación con logaritmos a ambos lados, no preocuparse, pues dentro de poco desaparecerán.

Lo primero que debemos hacer es convertir esa suma en multiplicación, por las propiedades de los logaritmos.

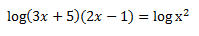
Resolvemos la multiplicación entre paréntesis:

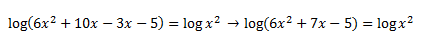
Ahora, al tener logaritmos en ambos lados, los eliminados y resolvemos como si fuese una ecuación normal:

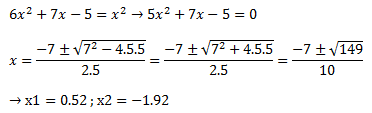
**Nota: las soluciones negativas no se consideran en los logaritmos, pues no existen logaritmos de números negativos, o lo que es lo mismo: ¿A qué número deberías de elevar otro para obtener un número negativo? Exacto, es imposible.

Ejemplo 3:

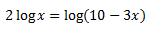
En este caso, tenemos que pasar ese dos como exponente, para poder eliminar los logaritmos:

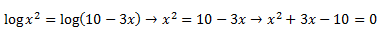
Ahora debemos resolver esa ecuación de segundo grado como siempre:

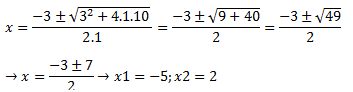
Descartaremos la solución x1=-5 al ser negativa.

Ejemplo 4:

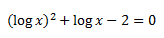
En esta ecuación, primero debemos efectuar una sustitución, cambiaremos el logx por t:

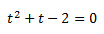
Ahora tenemos una ecuación de segundo grado, que resolvemos:

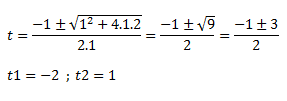
Después debemos hallar cuánto vale x:

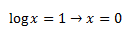
**Nota: no hemos considerado la solución t1 al ser negativa, pues no existe ningún logaritmo de números negativos.

Esperamos que estos ejemplos te hayan ayudado a entender mejor cómo resolver ecuaciones logarítmicas. Recuerda, la clave es utilizar las propiedades de los logaritmos para simplificar la ecuación y convertirla en una forma que puedas resolver. Con práctica, resolver ecuaciones logarítmicas se convertirá en una segunda naturaleza.