Ecuaciones irracionales

Una ecuación irracional no es más que una ecuación cuyas incógnitas están contenidas dentro de raíces, llamadas estas expresiones, radicales. Ejemplo:

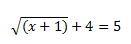
Para resolver este tipo de ecuaciones se procederá siempre de la misma manera, eliminando lo que nos molesta, los radicales. Esto se consigue elevando ambos miembros de la igualdad al índice de la raíz (es decir, si está con una raíz cuadrada, al cuadrado, si es una raíz cubica, al cubo, y así sucesivamente).

Vamos a realizar unos cuantos ejemplos resueltos para intentar explicarlo mejor:

Ejemplo 1:

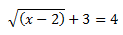
Nuestro objetivo es quitar esas molestas raíces, pero antes debemos asegurarnos de tener en ambos lados de la igualdad radicales y números según corresponda, es decir, en el ejemplo, antes de elevar todo al cuadrado, debemos pasar ese 3 restando al lado derecho, para simplificar la ecuación:

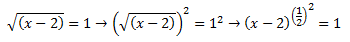
Hemos transformado la raíz cuadrada en potencia, para que podáis entender mejor el proceso.

Al elevar esa potencia (el radical) al cuadrado, nos quedaría dos partido por dos:

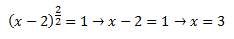
**Pista: Recordad que, al elevar un exponente a algo, se multiplica el exponente por el otro exponente al que lo tenemos que elevar, de ahí sale el 2/2. Es decir, ni se os ocurra pensar que se trata de elevar el 1/2 todo al cuadrado, el uno y después el dos , puesto que no lo tratamos como un numero, sino como un exponente, tenéis por tanto que recordar que estáis resolviendo una potencia.

Ejemplo 2:

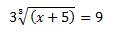
En este caso, el índice de la raíz es tres, pero no pasa nada, se resuelve igual que el anterior, tan solo que en este caso, hemos de elevar la raíz al cubo, para poder eliminarla, no os olvidéis de elevar también al miembro que está a la derecha:

 

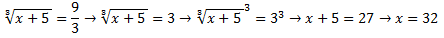
Ejemplo 3:

 

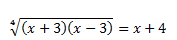
Bien, de principio no os asustéis por ver más datos de lo habitual, simplemente tendremos que simplificar un poco más al principio:

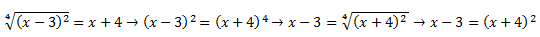
Al elevar todo a la cuarta, eliminamos la raíz, además, en el segundo paso hemos transferido el cuadrado del binomio (x-3) a la derecha, convirtiéndose en una raíz, que se elimina automáticamente y queda reducido el lado izquierdo de la igualdad a (x+4)^2

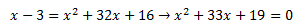
Después de desarrollar ese binomio al cuadrado, nos encontramos con una ecuación de segundo grado, que procedemos a resolver:

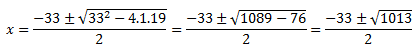
Como no podemos simplificar ese 10113 en potencias, se puede dejar así planteado, dentro del radical, separando las soluciones de x en x1 y x2:

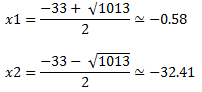
En ambos casos se ha provisto de un resultado aproximado, aunque como he dicho, a veces se recomiendo dejar así planteada la solución sin dar el resultado exacto.