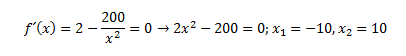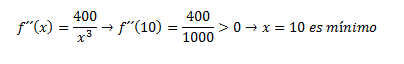Problemas de optimización

Como hemos mencionado en los artículos anteriores, una de las aplicaciones más importantes en las matemáticas es la resolución de problemas de optimación. Pero, ¿a qué nos referimos con problemas de optimización? ¿Cómo podemos resolverlos? No os preocupéis, porque estas y otras de vuestras inquietudes serán resueltas si continuáis leyendo.

DEFINICIÓN

Los problemas de optimización son aquellos que se ocupan de elegir la decisión óptima de un problema, es decir, encontrar cual es el máximo o mínimo de un determinado criterio (una función) sujeto a unas condiciones que nos da el problema.

PASOS PARA RESOLVER UN PROBLEMA DE OPTIMIZACIÓN

Para resolver un problema de optimización de forma correcta vamos a establecer una serie de pasos que nos harán más sencillo el planteamiento y la resolución:

1º. En primer lugar, establecemos cuál o cuáles son las incógnitas que nos plantea el problema.

2º. A continuación tenemos que buscar y plantear qué es lo que tenemos que maximizar o minimizar: f(x,y)

3º. Después buscamos la condición que se nos plantea. En la mayoría de los problemas que nos encontremos, la función a maximizar o minimizar dependerá de dos variables, por tanto la condición nos permitirá relacionar estas dos variables para poner una en función de la otra.

4º. Una vez, que hemos despejado una variable en función de la otra, supongamos y en función de x. Sustituimos en nuestra función a optimizar, quedándose ahora en función de una sola variable: f(x)

5º. Derivamos la función y la igualamos a cero: f´(x)=0.

6º. Una vez obtenidas las soluciones nos falta el último paso, comprobar si realmente se trata de un máximo o un mínimo, para ello, realizamos la segunda derivada de tal forma que:

– si f´´(x)0, entonces se trata de un mínimo.

7º. El último paso, una vez que ya tenemos x, sería irnos al paso 3, donde habíamos despejado y, y hallar el valor de y, y damos la solución.

EJEMPLOS

Una vez que ya hemos establecido unos pasos para llevar a cabo, vamos a resolver los siguientes problemas. Aunque parezcan muchos pasos, no os alarméis, se hacen de forma muy rápida y muchas veces podemos hacer varios a la vez. Seguiremos los pasos mencionados planteándolos en forma de pregunta. Para empezar haremos un problema facilito….

Problema 1: Encontrar dos números cuya suma sea 150 y el producto sea máximo.

1º. ¿Cuáles son nuestras incógnitas? Como buscamos dos números:

x: primer número

y: segundo número

2º. ¿Cuál es la función que tenemos que optimizar? Nos piden que el producto sea máximo, luego:

f(x,y) = x•y, máximo

3º. ¿Qué condición deben cumplir? La relación entre las dos variables es que suman 150:

x+y=150→y=150-x

4º. Sustituimos en la función a maximizar:

5º. Derivamos e igualamos a cero.

f´(x)=150-2x=0→x=75

6º. ¿Es el máximo? Lo comprobamos haciendo la segunda derivada.

f´´(x)=-2→x=10 es mínimo

7º. ¿Cuál es la solución? Una vez calculado x, nos vamos al tercer paso y sustituimos:

y=150-x=150-75=75

Luego, los número buscados son x=75 e y=75.

Problema 2: De entre todos los rectángulos de 100 m2 de área, encontrar las dimensiones del de perímetro mínimo.

1º. x: base del rectángulo

y: altura del rectángulo

2º. Hay que hallar el perímetro mínimo:

f(x,y)=2x+2y, mínimo

3º. La relación que nos dan es el área: x•y=100→y=100/x

4º. Sustituyendo:

f(x)=2x+2(100/x)

5º. Derivamos e igualamos a cero:

Como estamos en un problema de longitudes la solución negativa podríamos descartarla directamente.

6º. Comprobamos:

7º. Solución:

y= 100/10=10

Luego las dimensiones del rectángulo son 10m de base y 10m de altura (es un cuadrado).