Área del triángulo

Para comenzar tendremos que definir qué es un área, pues bien, un área no es más que lo que mide la región encerrada en una figura geométrica. En nuestro caso, gráficamente, el área del triangulo de se podría representar así:

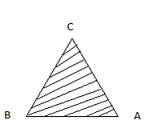
La parte rayada sería el área del triangulo ABC, y se mediría en unidades cuadradas ( metros cuadrados, etc.).

Para obtener esta área en concreto, de forma generalizada, debemos dividir el resultado del producto entre la base ( denominada b) y la altura del triangulo ( denominada como «h»). Puesto en forma gráfica:

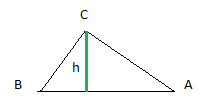
**Pista**: Como veis, la altura, es la recta perpendicular trazada desde un vértice a su lado opuesto, y pondremos una «h» en el lado izquierdo de esa recta para reconocerla como tal.

Cuya formulación sería:

A = (b* h)/2

Me gustaría antes de nada proponeros un pequeño problema para que os quede mejor la fórmula del área del triangulo:

*Pensemos en un cuadrado de 8 centímetros de lado, el área de un cuadrado es lado x lado =lado al cuadrado , por tanto, sería igual a8x8= 64 cm2.

Si trazamos una diagonal desde uno de los vértices del cuadrado hasta su vértice opuesto, obtendremos un triángulo que medirá 32 cm2.

De esto deducimos que el área del cuadrado es el doble que la del triángulo, y por eso el área del triangulo es base por altura dividido entre dos.

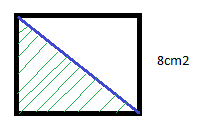
**Pista**: Si os fijáis la figura del cuadrado son dos triángulos pegados.

Además, es importante mencionar que existen diferentes tipos de triángulos y la forma de calcular el área puede variar dependiendo de la información que tengamos disponible. Por ejemplo, en un triángulo equilátero, donde todos los lados son iguales, podemos usar la fórmula A = (lado² * √3) / 4. En un triángulo isósceles, donde dos lados son iguales, podemos usar la fórmula A = (base * √((4 * lado²) – base²)) / 4.

Además, en un triángulo rectángulo, que tiene un ángulo de 90 grados, podemos usar la fórmula A = (base * altura) / 2, donde la base y la altura son los dos lados que forman el ángulo recto. Este es un caso especial donde la altura es uno de los lados del triángulo.

Dicho esto vamos a realizar un ejemplo aplicando lo visto anteriormente.

Supongamos un triangulo cuya base mide 7cm y la altura 4cm, ¿Cuál es su área?

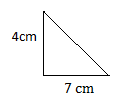
Aplicando la formula de arriba:

A = (b* h)/2 =( 7cm * 4cm)/2 = 28/2 cm2 = 14 cm2

Por tanto, la región que ocupa este triangulo si lo dibujásemos en un papel serían 14 cm2.

Hay muchas más formas de calcular el área de un triángulo, por ejemplo, si no nos diesen la altura o la base pero uno de los ángulos del triángulo, podríamos hallarlo gracias a los senos y cosenos, pero eso ya es trigonometría, y lo dejaremos para más adelante, por ahora quedaros con lo básico.

Además, es importante mencionar que el área de un triángulo también se puede calcular utilizando las coordenadas de sus vértices en un sistema de coordenadas cartesianas. Esta es una técnica muy útil en geometría analítica y en la resolución de problemas de física y ingeniería. La fórmula para calcular el área de un triángulo en este caso es A = 1/2 |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|, donde (x1, y1), (x2, y2) y (x3, y3) son las coordenadas de los vértices del triángulo.

Finalmente, es importante recordar que la fórmula del área de un triángulo es una de las fórmulas más básicas y fundamentales en geometría. Es una herramienta esencial para resolver una amplia variedad de problemas matemáticos y se utiliza en muchas áreas diferentes de la ciencia y la ingeniería.