Método de la secante

Este método es usado en el análisis numérico, para encontrar las raíces de una función, mediante iteracciones. Es una técnica que se utiliza en la resolución de ecuaciones no lineales y se considera un método abierto, es decir, no se requiere un intervalo que contenga la raíz.

Tiene ciertas ventajas frente a otros métodos, como por ejemplo, que no necesitamos saber la primera derivada (newton) y se procede independientemente a los signos de la función (a diferencia del método de la regla falsa). Además, tiene un gran índice de aciertos, al considerar solamente dos puntos al principio. Este método es especialmente útil cuando la derivada de la función es difícil de calcular o cuando se quiere una solución aproximada rápidamente.

Se basa en ir trazando rectas secantes a la curva de la función buscada, y se va comprobando la intersección de estas con el eje x para ver si es la raíz que buscamos. Este proceso se repite hasta que se alcanza un nivel deseado de precisión.

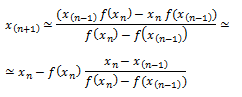
Es por tanto necesario el conocimiento de dos valores, que se utilizan como puntos de partida para el método. Estos dos valores deben ser elegidos de manera que estén cerca de la raíz que se busca.

Seguramente nos den un ∈ y nos pedirán que aproximemos la raíz hasta que sea menor a éste. Este valor representa el error tolerable en la solución. Cuanto más pequeño sea este valor, más precisa será la solución obtenida, pero también requerirá más iteraciones para alcanzar ese nivel de precisión.

Como veis es muchísimo más sencillo que los anteriores, tan solo hemos hallado el valor de la función en 2 puntos, hemos sustituido en la fórmula de la secante, y comprobamos nuestros error aproximado. Hay que destacar, que dicha función es una aproximación que se hace a la primera derivada, ahorrándonos el cálculo de ésta, que si os fijáis, no es nada más y nada menos que la pendiente que une los dos puntos a considerar.

El método de la secante es una excelente opción cuando se necesita una solución rápida y aproximada. Sin embargo, hay que tener en cuenta que no siempre converge, especialmente si los valores iniciales no están cerca de la raíz. En estos casos, puede ser necesario utilizar otros métodos, como el de bisección o el de Newton.

Además, aunque el método de la secante generalmente requiere menos iteraciones que el método de bisección, cada iteración es más costosa computacionalmente, ya que implica más cálculos. Por lo tanto, la elección del método a utilizar dependerá de las características específicas del problema a resolver.

>>Ejemplo:

Usar el método de la secante para aproximar la raíz de:

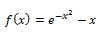
Comenzando con x0=0 y x1=1, y hasta que |Ea|<1%

Procedemos a resolver el ejercicio:

1º) Sustituimos los valores de x en la función:

f(x0)=1

f(x1)= -0.632120558

2º) Sustituimos, en la fórmula de la secante esos valores, para calcular la primera aproximación, que denotamos como x2:

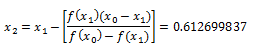
3º) Calculamos el error aproximado:

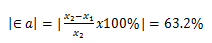
4º) Todavía no cumplimos nuestro objetivo, así que nos tocaría repetir el proceso de nuevo desde el paso 1, usando x1 y x2 en vez de x0, hallando un nuevo punto, que llamaríamos x3, y así sucesivamente.

A continuación os pego la tabla con los resultados. La primera columna son los «x», y la segunda los errores relativos (Ea).

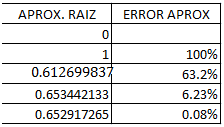
Por tanto, concluimos que la aproximación de la raíz es x4=0.652917265 con un |Ea|=0.08%

Este ejemplo demuestra cómo el método de la secante puede ser utilizado para encontrar una solución aproximada a una ecuación no lineal. Aunque el método puede parecer un poco complicado al principio, con un poco de práctica se vuelve bastante sencillo de implementar. Además, la capacidad de este método para proporcionar soluciones rápidas y aproximadas lo convierte en una herramienta valiosa en muchas áreas de la ciencia y la ingeniería.