Dependencia e independencia lineal

Dados los números siguientes, a1, a2, …, an y los vectores v1, v2, …, vn, llamamos combinación lineal a cada uno de los vectores, de esta forma:

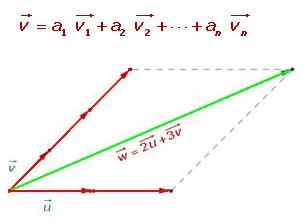
Cualquier vector puede ponerse como combinación lineal de otros dos que posean diferente dirección.

Sea {v1, v2,…, vn} un conjunto de vectores. Podemos decir que son linealmente dependientes si existen números tales como «a1, a2,…, an, no todos iguales a cero, de modo que:

Podemos observar que el símbolo a la derecha del signo igual no corresponde a cero, sino que en cambio simboliza al vector nulo. El conjunto de vectores nulos forma lo que se llama matriz nula. Si tales números no están, entonces los vectores serán linealmente independientes. Si manejamos el concepto de espacios vectoriales podemos determinar la independencia lineal de esta forma:

Un conjunto de vectores U perteneciente a un espacio vectorial será linealmente independiente si:

Es importante tener en cuenta esto, ya que los conjuntos de vectores linealmente independientes y que generan un espacio vectorial, forman también una base para el espacio vectorial. Como propiedades de los vectores linealmente dependientes e independientes podemos subrayar lo siguiente:

Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los otros.

Si un conjunto de vectores es linealmente independiente cualquier subconjunto suyo lo es también.

Si tenemos un conjunto de vectores y ninguno de estos es combinación lineal de los demás, seleccionando solamente unos cuantos, no podrán ser combinación de los demás.

Si un conjunto de vectores es linealmente dependiente también lo es cualquier conjunto que lo contenga.

Un conjunto de vectores es linealmente dependiente si y solo si tiene algún vector que sea combinación lineal de los demás, si introducimos este conjunto de vectores en otro mayor, seguimos obteniendo el vector que es combinación lineal de otros, por lo cual, el conjunto más grande seguirá siendo linealmente dependiente.

Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.

Dos vectores del plano son linealmente dependientes si sus componentes son proporcionales.

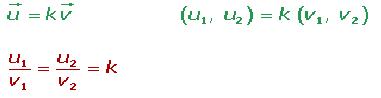
Muchos vectores libres del plano son linealmente dependientes si se halla una combinación lineal de ellos que sea igual al vector cero, sin que sean cero el total de coeficientes pertenecientes a la combinación lineal.

Si hablamos de vectores libres linealmente independientes, estamos hablando de aquellos que se pueden expresar como combinación lineal de los otros.

a1 = a2 = … = an = 0

Los vectores linealmente independientes tienen una dirección distinta.