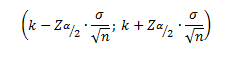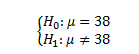Contraste de hipótesis
Una vez que ya hemos estudiado los intervalos de confianza, pasamos a estudiar los contrastes de hipótesis para una población.
¿PARA QUÉ UTILIZAMOS LOS CONTRASTES DE HIPÓTESIS?
Los contrastes de hipótesis se utilizan para afirmar o negar (aceptar o rechazar) un enunciado (hipótesis) a partir de una realización muestral de la población que queremos estudiar.
DEFINICIONES:
Un contraste de hipótesis para la media se basa en la formulación de dos hipótesis denominadas hipótesis nula (Ho) e hipótesis alternativa (H1). La hipótesis nula es la hipótesis que se supone cierta en el enunciado de nuestro problema (por contradictorio que parezca) y la hipótesis alternativa será todo lo contrario. De tal forma que nos encontramos con dos tipos de contrastes:
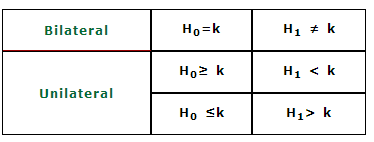
– Contrastes bilaterales: Son aquellos en los que la hipótesis nula expresa que la media es igual a un valor, y por tanto la hipótesis alternativa será que la media sea distinto a ese valor.
– Contrastes unilaterales: Los contrastes unilaterales, expresan una desigualdad, por tanto nos encontramos con dos tipos.
Una vez planteado el contraste de hipótesis, tenemos que seleccionar una región de aceptación, es decir si nuestra media muestral se encuentra dentro de esa región de aceptación aceptaríamos la hipótesis nula, y en caso contrario se rechazaría.
Para ello, se fija un nivel de significación: α.
La región de aceptación será un intervalo, que para ser más exactos en el caso del contraste bilateral coincide con el intervalo de confianza para la media a un nivel de confianza 1- α.
De tal forma que si tenemos un contraste de hipótesis bilateral, la región de aceptación será:
Mientras que para los contrastes unilaterales, dependiendo del tipo que sea, la región de aceptación será:
-Si la hipótesis nula es: Ho: µ≥k, entonces la región de aceptación es:
– Si la hipótesis nula es: Ho: µ≤k, entonces la región de aceptación es:
PASOS A SEGUIR A EN LA RESOLUCIÓN DE UN PROBLEMA:
Vamos a establecer unos pasos para plantear los problemas:
1. Determinar cuál es la hipótesis nula (Ho) y cuál es la hipótesis alternativa (H1).
2. Indicar el nivel de significación, α, y hallar el valor crítico.
3. Indicar el tamaño de la muestra que estamos estudiando.
4. Calcular la región de aceptación.
5. Tomar la decisión adecuada.
Finalmente, como es costumbre, vamos a realizar un ejemplo:
Ejemplo: Sabemos que la edad de los trabajadores de una determinada franquicia en el momento de su apertura tiene un comportamiento Normal con media 38 años y desviación típica 4. Una empresa de esta franquicia que se ha instalado en España, ha contratado sólo 150 empleados y ha comprobado que la edad media de sus trabajadores es de 38.3 años. ¿Se puede aceptar que la edad media de los trabajadores de esa franquicia es la misma en España que en Europa, para un nivel de significación del 5%?
Siguiendo los pasos que hemos determinado anteriormente:
1. En primer lugar indicamos la variable que estamos estudiando:
X=”Edad de los trabajadores de una franquicia” → N(38;4)
2. Determinamos nuestra hipótesis nula e hipótesis alternativa:
Como podemos observar se trata de un contraste bilateral:
3. El nivel de significación: α=0,05, por tanto el valor crítico es: ![]()
4. El tamaño de la muestra que estamos estudiando es n=150
5. La región de aceptación es:
6. Por último tenemos que tomar una decisión, es decir si la media muestral está dentro de nuestra región de aceptación.
En este caso, 38,3 está dentro de nuestra región de aceptación, por tanto, aceptamos la hipótesis nula, es decir, se puede afirmar que la edad media de los trabajadores es la misma en España que en el resto de Europa.