Producto exterior
En álgebra lineal, el producto exterior se refiere característicamente al producto tensorial de dos vectores. El resultado de aplicar el producto externo a un par de vectores es una matriz. El contraste de la denominación productor exterior con producto interno, es tomado como entrada al par de vectores y produce un escalar.
Otras generalizaciones del producto exterior pueden realizarse por ejemplo en los tensores. El producto externo es también una función de alto orden u orden superior, comúnmente estas funciones se denominan funcionales u operadores.
Multiplicación de la matriz
El producto externo de vectores es un caso especial del Producto de Kronecker de matrices.
Dado el vector de la columna y vector de la fila , el producto exterior de estos vectores es a la vez un producto tensorial (puesto que el producto exterior como ya hemos dicho es el producto tensorial de dos vectores) y da como resultado una matriz en bloque. Si A es una matriz m.x y B es una matriz p.q, el producto de Kronecker A x B es la matriz en bloque mp x nq,
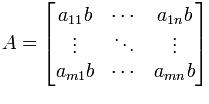
Más explícitamente, tenemos,

Veamos un ejemplo,

Teoría de Grassmann
Grassmann utilizó las álgebras reales, aquellas en las cuales los escalares son los números reales. Daremos aquí las definiciones para algunos de sus productos:
Un producto es una función lineal del producto tensorial de un espacio con sí mismo en un espacio lineal. Siendo así, el producto es distributivo, pero puede no ser asociativo.
Producto exterior:
Sea { ei } una base de un espacio vectorial V. Un producto exterior, o producto cuña, de dos tales generadores se define requiriendo las reglas de cómputo (relaciones) siguientes:
![]()
Se amplía este proceso como un recurso, a los productos de un grado más alto
![]()
El producto puede tomar valores en un nuevo espacio V ^ V (índice doble) que sea un espacio factor del producto tensorial,![]()
El producto es asociativo por definición y alternante, o sea que se anula si dos índices son equivalentes.
Un cálculo combinatorio breve manifiesta que es posible obtener de n vectores de base 2 a la n, productos que sean linealmente independientes.
Construyen el espacio V^ vectorial subyacente a un álgebra de Grassmann. El producto exterior se extiende hacia el espacio entero V ^por bilinealidad.
Un álgebra de Grassmann es lo que se dice un álgebra graduada o un álgebra sobre un cuerpo (por ejemplo un espacio vectorial A sobre K equipado con una noción compatible de multiplicación de elementos de A)
Podemos definir el grado de los escalares como cero y el grado de los vectores de base como 1. El grado de un producto diferente a cero de generadores cuenta el número de generadores.
El espacio de un álgebra de Grassmann se puede entonces descomponer en una suma directa de subespacios homogéneos de grado definido, o sea el espacio propagado por todos los productos que tienen puntualmente k generadores:
![]()
![]()
