Producto tensorial
En matemáticas, el producto tensorial, puede ser aplicado en diversos contextos a vectores, matrices, tensores, espacios del vector, álgebra, espacios topológicos del vector, y módulos. En cada caso la significación del símbolo se utiliza de la misma fórmula. El caso más general es el de operación bilineal, un operador bilineal es una multiplicación «generalizada» que cumple con la propiedad distributiva.
En algunos contextos, este producto también se refiere al producto externo. El término “producto tensorial” además se utiliza en lo referente a categorías monoidales o categorías de tensores.
Un caso representativo es el producto de Kronecker de cualesquiera dos matrices. Por ejemplo:
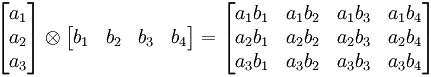
Rango resultante = 2, Dimensión resultante = 3×4.
Aquí el rango indica el número de índices indispensables, mientras que la dimensión cuenta el número de grados de libertad en el arreglo resultante.
Producto tensorial de dos tensores
Es importante saber que un tensor es cierta clase de entidad algebraica de varias componentes, que generaliza los conceptos de escalar, vector y matriz de una manera que sea independiente de cualquier sistema de coordenadas elegido. Los tensores pueden ser representados por una matriz de componentes en algunos casos. Existe una fórmula particular para el producto de dos (o más) tensores, que sería,
Con esto se esta asumiendo, para simplificar, tensores ortogonales, (la ortogonalidad es una generalización de la noción geométrica de perpendicularidad) sin distinción entre índices covariantes y contravariantes.
Los parámetros que se introdujeron arriba trabajan de la siguiente forma,
Producto Tensorial de Espacios Vectoriales
El producto tensorial,
es isomorfo a las matrices de entradas complejas de n por m (en el caso real también pasa lo mismo, el producto es isomorfo a las matrices de n x m reales).
Sean V y W dos espacios vectoriales complejos de dimensión finita. La idea del producto tensorial es construir el mapa bilineal más general posible con dominio . Debemos recordar que un mapa f:VxW→ X (donde también X es un espacio vectorial) es bilineal si es lineal en cada una de las coordenadas.
La expresión “más general posible” hace referencia a que los valores de f no cumplan ninguna relación, exceptuado las impuestas por la bilinealidad.
El mapa bilineal super general existe y la dimensión del codominio tiene que ser mayor o igual al producto de la dimensión de V y la dimensión de W. Por lo cual tenemos la siguiente definición, Para el Producto tensorial de espacios vectoriales de dimensión finita.
Sean Vy W dos espacios vectoriales de dimensión finita. El producto tensorial V⊗W es un espacio vectorial de dimensión dim(V)dim(W) que está dotado de una función bilineal ⊗: V x W→V⊗W (la imagen de (v,w) por ⊗ se denota v⊗w ) tal que si { v1} es una base de y{wj} es una base de se tiene que { v1 ⊗ wj } es una base de V ⊗ W. La dimensión del producto tensorial por lo tanto es el producto de dimensiones.
Propiedad universal del producto tensorial
Sea G un grupo abeliano, R un anillo unitario, M un R-módulo a derechas, N un R-módulo a izquierdas y f: M xN→G, una aplicación R-equilibrada. Si M y N los consideramos sólo como grupos abelianos, entonces,
Si fuesen M y N espacios vectoriales, entonces R sería un cuerpo, si M y N fuesen espacios vectoriales reales, sería,
Existe un único homomofismo de grupos,
de manera que,
cualesquiera que sean,
Particularización a espacios vectoriales reales.
El espacio de todos las funciones bilineales desde V x W a R es naturalmente isomorfo al espacio de todos las funciones lineales de V⊗W a R. Esto es por construcción:
V⊗W tienen exclusivamente las relaciones que son precisas para cerciorarse de que un homomorfismo de los V⊗W a R sea bilineal.
