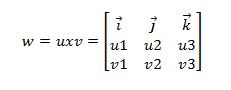Producto vectorial
A pesar de haber utilizado ya anteriormente el producto vectorial en el desarrollo de algunos de los temas vistos, nunca antes habíamos definido propiamente este concepto.
Ha llegado el momento de conocer su definición y propiedades, así como su interpretación geométrica y sus usos.
Definición:
Consideramos en el espacio vectorial V3 una base B={e1,e2,e3}. Dados dos vectores u y v de V3, definimos el producto vectorial de u por v ( u x v) como un nuevo vector w tal que:
1. El módulo del producto vectorial es igual al producto de los módulos del vector u por el módulo del vector v por el valor absoluto del seno de ángulo que forman ambos vectores, es decir:
|u x v|=|u||v||sen (u,v)|
2. El vector resultante, w, es perpendicular a u y a v, es decir, su producto escalar es 0.
wu= (u x v) u =0 y wv= (u x v) v=0
3. La terna formada por los vectores {u, v, w} tiene la misma orientación que la base del espacio vectorial B={e1,e2,e3}, es decir, los signos de los determinantes de cada una de la ternas son iguales. Esta condición se pone de manifiesto en la famosa regla del sacacorchos utilizada en física para determinar la dirección del campo magnético.
El producto vectorial se calcula normalmente utilizando la expresión en forma de determinante (aunque realmente no es un determinante propiamente dicho). De tal forma que sean u=(u1,u2,u3) y v= (v1,v2,v3) el producto vectorial uxv, se calcula:
Propiedades:
Vamos a ver las propiedades que cumple el producto vectorial, las cuales se demuestran utilizando la expresión en forma de determinante, por tanto estarán relacionadas con las propiedades de los determinantes:
a) El producto vectorial de un vector por sí mismo es 0: u x u = 0
b) Si el producto vectorial de dos vectores distintos entre sí, y distintos de cero es cero; entonces los vectores son paralelos:
El recíproco también es cierto, es decir, si u y v son paralelos, entonces
u x v =0.
c) El producto vectorial es anticonmutativo, al cambiar el orden del producto se cambia el signo:
u x v = – (v x u)
d) Podemos decir que se cumple la propiedad distributiva respecto de la suma de vectores:
u x (v+w)= u x v + u x w
e) Para todo α perteneciente a los números reales : u x (αv) = (αu) x v= α ( u x v)
f) El producto vectorial de cualquier vector con el vector nulo 0 = (0,0,0) es 0:
u x 0=0
Interpretación geométrica
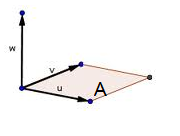
El módulo del producto vectorial de dos vectores (|u x v|) coincide con el área del paralelogramo que tiene por lados u y v.
Área del paralelogramo = | u x v|
Aplicaciones en problemas geométricos y físicos
Algunas de las aplicaciones más importantes son:
– Hallar la distancia entre dos rectas que se cruzan:
Sea r una recta determinada por el punto A y el vector u, y sea s una recta determinada por el punto B y el vector v, la distancia entre r y s viene dada por:
– Hallar el momento angular:
El momento angular de una partícula de masa m aparece en el estudio del movimiento curvilíneo, viene dado por:
donde r es el vector de posición de la partícula, m la masa de la partícula y v la velocidad a la que se mueve.