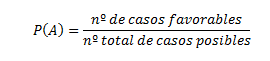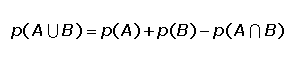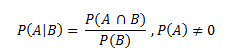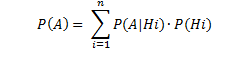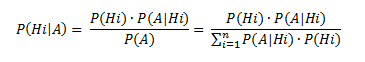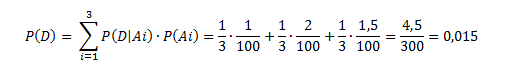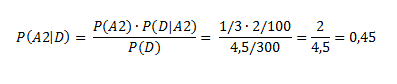Probabilidad de un suceso
A lo largo de este post, nos vamos a centrar en cómo calcular la probabilidad de un suceso aleatorio y algunas de sus propiedades más útiles.
Denotamos al espacio probabilístico por Ω, sea A un suceso aleatorio del espacio. Para calcular la probabilidad de A, utilizamos la famosa regla de LaPlace:
Ejemplo: Calcular la probabilidad de sacar un número impar al tirar un dado:
El espacio probabilístico está formado por todos los números posibles:
Ω ={1,2,3,4,5,6}
Entonces la probabilidad de A es:
P(A)=3/6=0,5
PROPIEDADES DE LA PROBABILIDAD
1. La probabilidad siempre toma valores entre 0 y 1: 0≤P(A)≤1
2. La probabilidad del espacio muestral es 1: P(Ω)=1
3. La probabilidad del vacío es 0: P(ø)=0
4. La probabilidad del suceso contrario de A es:
5. La probabilidad de la unión de sucesos (A U B):
6. Si A es un subconjunto de B, la probabilidad de A es menor o igual que la de B.
Además de estas propiedades, es importante mencionar que la probabilidad también cumple con la propiedad distributiva y conmutativa. Esto significa que la probabilidad de la unión de dos sucesos es igual a la suma de las probabilidades de cada uno de ellos, menos la probabilidad de su intersección. De manera similar, la probabilidad de la intersección de dos sucesos es igual a la probabilidad de uno de ellos, multiplicada por la probabilidad del otro, dado el primero.
PROBABILIDAD CONDICIONADA
En algunas situaciones, la probabilidad de un suceso determinado, A, se ve afectada por otro suceso diferente. Por tanto, cuando queremos estudiar la probabilidad de un suceso A sabiendo que se ha dado otro suceso B, estamos hablando de probabilidad condicionada.
Definimos la probabilidad de A condicionada a que haya ocurrido B P(A|B) como :
Propiedades de la probabilidad condicionada:
1. Si A y B son independientes: P (A|B) = P(A)
2. Si A y B son incompatibles: P(A|B) = 0, ( ya que si A y B son incompatibles la intersección es el vacío)
3. P(A│B)+P(Â|B) = 1
4. P( Ω|B) = 1
TEOREMA DE LA PROBABILIDAD TOTAL
Sean H1, H2,……., Hn sucesos disjuntos, con probabilidad no nulas cuya unión es el espacio muestral Ω, se define la probabilidad de un suceso cualquiera A, como:
Donde los sucesos Hi se denominan hipótesis o causas, P(Hi) se llaman probabilidad a priori y P(Hi|A) es la probabilidad a posteriori.
TEOREMA DE BAYES
Para terminar el estudio de la probabilidad, nos queda por ver el Teorema de Bayes, en el que se mezclan, por decirlo de alguna manera la probabilidad condicionada y el teorema de la probabilidad total.
Este teorema, se utiliza para calcular la probabilidad a posteriori de una hipótesis Hi, sabiendo que ha ocurrido un suceso cualquiera A:
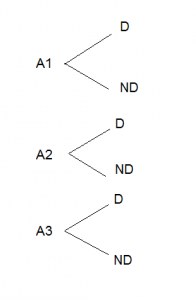
Ejemplo: Una tienda de bolígrafos recibe materiales de tres fábricas diferentes: A1, A2, y A3. En cada una de ellas hay una probabilidad de que un bolígrafo sea defectuoso de un 1%, 2% y 1,5% respectivamente.
a) ¿Cuál es la probabilidad de que un bolígrafo seleccionado al azar sea defectuoso?
b) Si compramos un bolígrafo, y resulta que este es defectuoso, ¿cuál es la probabilidad de que proceda de la fábrica A2?
La forma más visual de enfrentarnos a este problema es a través de un diagrama de árbol que nos muestre un esquema del problema; donde A1, A2 y A3 son nuestras hipótesis:
P(A1)= 1/3, P(A2)=1/3 y P(A3)=1/3
P(D|A1) = 1/100, P(D| A2)= 2/100, P(D|A3) = 1,5/100
Con estos datos ya podemos calcular lo que nos piden:
a) Utilizando el teorema de la probabilidad total:
b) Utilizando el teorema de Bayes:
En el mundo real, la probabilidad se utiliza en una amplia variedad de disciplinas, desde la meteorología hasta la economía y la medicina. Por ejemplo, en medicina, se utilizan pruebas de diagnóstico para determinar la probabilidad de que un paciente tenga una determinada enfermedad. En economía, se utilizan modelos probabilísticos para predecir el comportamiento de los mercados financieros. En meteorología, se utilizan modelos probabilísticos para predecir el clima. En cada uno de estos casos, el objetivo es tomar decisiones informadas basadas en la probabilidad de diferentes resultados.