Ley potencial
Un fenómeno físico responderá a una ley potencial cuando las probabilidades de que acontezca sierto suceso, declinan de modo eventual, con determinada magnitud, es decir siguiendo una fórmula como la siguiente,
![]()
x corresponde a una variable aleatoria medible que se eleva a una potencia.
Una ley potencial es entonces un determinado tipo de relación matemática entre dos cantidades. si dichas cantidades son correspondientes a lo que se llama variable aleatoria (que es una función) y también a su frecuencia. En una distribución de ley de potencias, las frecuencias pueden llegar decrecer a causa del exponente si la variable aleatoria aumenta.
Hay muchos fenómenos naturales que cumplen con lo dicho anteriormente. Un buen ejemplo es el de los terremotos. Si procedemos a dibujar en un gráfico el número de veces que hay terremotos, en función de la energía que se libera, obtendremos entonces una curva de tipo potencial como se muestra en la siguiente imagen:

Si observamos la zona alta de la curva, podemos sacar la conclusión de que han habido gran cantidad de terremotos de poca dimensión, mientras que si observamos la zona baja de la curva nos damos cuenta de que hay poca cantidad de terremotos de gran dimensión. Este es un buen ejemplo de la escencia de la Ley potencial, la cual es, “muchos con poco y pocos con mucho”. Los sucesos acontecen con una frecuencia variable, siendo la mayoría de estos, de pequeña escala y en menor medida, de gran escala.
Esta Ley tiene una gran inclinación hacia los valores extremos, de modo que los acontecimientos de gran dimensón tienen una gran probabilidad de incidencia. Este tipo de distribuciones son posibles de hallar en sistemas artificiales, naturales y sociales.
Otro ejemplo de ley potencial podría ser la relación que hay entre el número de ciudades y el número de habitantes, ya que hay pocas metrópolis y muchas ciudades pocos pobladores. También la perioricidad de las palabras en el lenguaje, la economía, etc. Estos son fenómenos bastante circunstanciales en distribución, por lo cual en una gráfica se esperaría obtener una curva de campana o gaussiana, como la que se muestra a continuación.
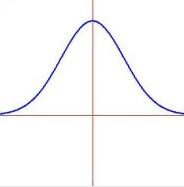
Esta es realmente distinta a una ley potencial, por lo cual es de suma importancia tener el conocimiento de si un suceso físico es correspondiente a una ley o la a otra. La curva campana aparece si el fenómeno físico tiende al valor central. Esta es una curva exponencial, por lo cual decae rápidamente si se aleja del valor central. Siendo así es un poco dificil hallar sucesos con gran diferencia. Un ejemplo de esto, sería decir que las probabilidades de hallar un ser humano de 8 metros de altura o 15 centímetros de altura son nulas, por esta razón la curva y nuestra intuición coincidirían. De forma distinta, una ley potencial no posee valor central. Las probabilidades también declinan pero de forma mas lenta que en el caso de la ley exponencial. Se puede cometer una equivocación si se cree que un fenómeno físico cumple con la ley exponencial y luego puede resultar ser ley potencial. Siendo así subestimaríamos la probabilidad de que suceda una órden de magnitud.
