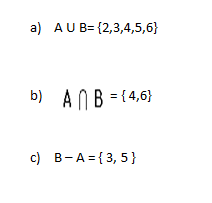Sucesos aleatorios

El azar y la probabilidad están presentes en nuestro día a día, cuando echamos la quiniela, jugamos al parchís, tiramos una moneda… y un largo etcétera.

Para poder trabajar en el campo de la probabilidad es necesario definir el espacio probabilístico o espacio muestral en el que estamos trabajando, así como los sucesos aleatorios que lo forman.

TIPOS DE SUCESOS ALEATORIOS:

Si denotamos al espacio muestral como Ω, tenemos los siguientes tipos de sucesos:

a) Suceso elemental: cada uno de los sucesos que forman el espacio muestral.

b) Suceso compuesto: cada uno de los subconjuntos formados por sucesos elementales que, evidentemente, son subconjuntos del espacio muestral.

c) Suceso seguro: como su nombre indica, engloba todos los sucesos posibles del espacio muestral.

d) Suceso imposible: al contrario que el anterior, y también como indica su nombre, es aquel suceso que no tiene ningún elemento y que denotamos por el vacío: ø.

Ejemplo: Escribir un suceso de cada tipo si tiramos un dado:

El espacio muestral es: Ω= {1,2,3,4,5,6}

a) Suceso elemental: A={sacar un 2}

b) Suceso contario: Â= {no sacar un 2}

c) Suceso compuesto: B={sacar un número impar}

d) Suceso seguro: C={sacar un número menor que 8}

e) Suceso imposible: D={sacar un número mayor que 10}

OPERACIONES CON SUCESOS:

Al igual que con los números, con los sucesos también podemos operar:

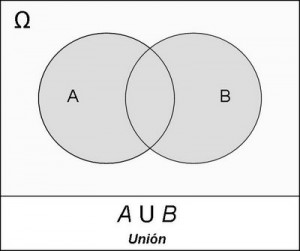
a) Unión de dos sucesos: Definimos la unión de los sucesos A y B como un nuevo suceso formado tanto por los elementos de A como por los de B, sin repetir los elementos que estén en los dos. Este concepto se puede extender a la unión de n sucesos.

Propiedades de la unión de sucesos:

1. Idempotente: A U A = A

2. La unión de sucesos es conmutativa: A U B = B U A

3. La unión de sucesos es asociativa: (A U B) U C = A U (B UC)

4. La unión de un suceso y su contrario es igual al espacio muestral: A U Â= Ω

5. La unión de un suceso y el espacio muestral es el espacio muestral: A U Ω = Ω

6. La unión de un suceso y el vacío es el suceso, es decir, el vacío es el elemento neutro para la unión: A U ø = A

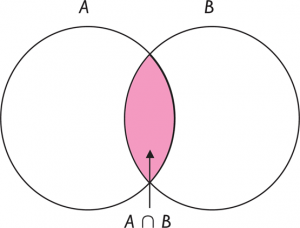
b) Intersección de dos sucesos: Definimos la intersección de los sucesos A y B como un nuevo suceso formado por los elementos que son comunes a ambos sucesos, es decir, los que pertenecen tanto al suceso A como al suceso B.

1. Idempotente:

2. La intersección de sucesos es conmutativa:

3. La intersección de sucesos es asociativa:

4. La intersección de un suceso y su contrario es igual al vacío:

5. La intersección de un suceso y el espacio muestral es el suceso, es decir el espacio muestral es el elemento neutro para la intersección:

6. La intersección de un suceso cualquiera y el vacío es el vacío:

A partir de las definiciones de unión e intersección también se cumplen las siguientes propiedades:

1. La unión es distributiva respecto de la intersección:

2. La intersección es distributiva respecto de la unión: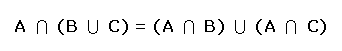

c) Diferencia de sucesos ( B – A) : Es el suceso formado por los elementos de B que no están en A.

Propiedades de la diferencia de sucesos:

Ejemplo: Sean los sucesos aleatorios: A={sacar un número par al tirar un dado} y B={sacar un número mayor o igual que 3 al tirar un dado}. Halla los siguientes sucesos:

En primer lugar vamos a obtener los números que forman estos sucesos:

A= {2,4,6} y B ={3,4,5,6}