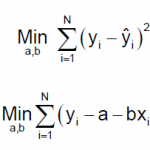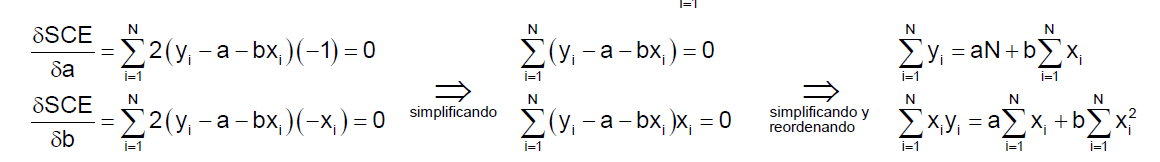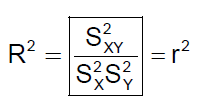Rectas de regresión

Para poder estimar el valor de una variable a partir de otra variable independiente dados unos datos previos, utilizamos la recta de regresión, siempre y cuando las variables estén relacionadas de forma dependiente.

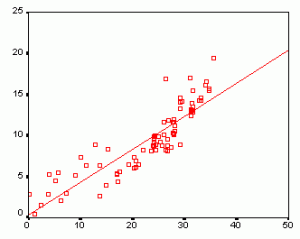
Los valores de las variables se pueden representar mediante una nube de puntos, por tanto la recta de regresión es el modelo lineal que más se acerca a la relación entre las variables, como podemos ver en la siguiente imagen:

REGRESIÓN LINEAL MÍNIMO CUADRÁTICA Y/X

Cuando la nube de puntos se puede aproximar mediante una recta, hablamos de regresión lineal y esta aproximación vendrá dada por la siguiente expresión: Y´=a+bX, ya que existe dependencia lineal. Realmente lo que podemos calcular a partir del valor de xi es un valor aproximado de la verdadera yi, por eso lo denotamos por y´.

El coeficiente b se denomina coeficiente de regresión, y el coeficiente a es el punto de corte con el eje Y.

A la diferencia entre el valor real u observado:y; y su aproximación mediante la recta y´, es decir el valor estimado o ajustado, se le denomina residuo o error y lo denotares por ei=yi-yi´.

Para poder obtener la recta de regresión por el método de mínimos cuadrados haremos mínima la suma de los cuadrados de los residuos. Por tanto el problema que tendríamos que resolver es el siguiente:

Vamos a calcular los parámetros a y b que minimizan esta última expresión a la que llamaremos SCE. Para ello derivamos en función de a y b respectivamente, igualamos a cero y resolvemos el sistema que forman sus derivadas:

Por último, dividiendo por N (el tamaño de la muestra) y despejando a y b obtenemos sus valores:

RECTA DE REGRESIÓN X/Y

Análogamente, estimando en este caso el valor de x en función de la y, obtendríamos la recta de regresión de x sobre y: X´=a´+b´Y, donde en este caso los valores de a´y b´son:

BONDAD DEL AJUSTE

Llamamos correlación al grado de dependencia que existe entre ambas variables. Si la función se ha ajustado mediante regresión y pasa por todos los puntos, lo que querrá decir que no hay residuos o errores; el grado de dependencia es el máximo posible. Por el contrario, también puede ocurrir que los residuos sean muy grandes y por tanto la dependencia será menor y también será menor la bondad del ajuste.

Para medir el grado de dependencia o la bondad del ajuste podemos utilizar dos coeficientes: el coeficiente de correlación lineal y el coeficiente de determinación:

-Coeficiente de correlación lineal:

El coeficiente de correlación lineal, r; que viene dado por el cociente de la covarianza entre el producto de ambas desviaciones típicas: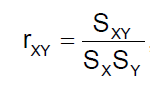

El valor que puede tomar es entre -1 y 1, cuanto más cerca de 1 o -1 esté la relación lineal es más perfecta o ajustada. Podemos resumirlo en los siguientes casos:

-Si r=1, la relación lineal es perfecta y positiva.

-Si r=-1, la relación es lineal perfecta y negativa.

-Si r=0, no existe relación lineal.

-Cuando -1<r<0, la relación lineal es negativa.

-Cuando 0<r<1, la relación lineal es negativa.

Si la relación lineal es positiva, quiere decir que si una variable aumenta la otra también o viceversa, cuando una disminuye también lo hace la otra. En cambio cuando la relación lineal es negativa, si una variable aumenta la otra disminuye o al contrario.

Cuando |r|>0,866 diremos que la relación lineal es buena.

-Coeficiente de determinación lineal:

Otro coeficiente que utilizaremos para estudiar la bondad del ajuste es el coeficiente de determinación, que no es otro que el coeficiente de correlación lineal al cuadrado:

Puede tomar los valores entre el 0 y el 1. Cuanto mayor sea el coeficiente, es decir más se acerque a 1, mayor será la dependencia lineal, considerando que el ajuste es bueno cuando sea mayor que 0,75.

La única diferencia con el coeficiente de correlación lineal es que este coeficiente no nos permite calcular si la relación es positiva o negativa, pero esto no siempre será necesario.