Pendiente de una recta
En la vida real, cuando vamos por la calle, a veces nos encontramos ante cambios en la nivelación del terreno, es decir, cuando íbamos por una calle totalmente recta y horizontal, de repente la calle empieza a «subir» verticalmente, inclinándose de forma vertical. A esta inclinación se le llama pendiente. Veámoselo en un ejemplo:
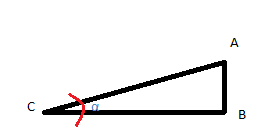
A, B y C son los puntos que forman la figura, siendo la distancia que hay de CB hasta CA la inclinación del triangulo, que coincide con la altura, en este caso, y que llamaremos incremento de h.
Una cosa que me gustaría que recordarais es que la pendiente es la derivada de la recta tangente a una curva. Esto os va a servir de mucho a la hora de mirar las derivadas.
Por tanto, la pendiente no es más que un cambio en un sistema de referencia (como un eje de abscisas y ordenadas) y que viene representado por la letra m, cuya fórmula es:
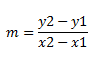
Siendo y2 e y1 el punto de origen y destino en dicho eje, así como en el de las equis. Si os fijáis, las abscisas(las «y») indican la altura de la recta, y las ordenadas(las «x») indican cuando se desplaza horizontalmente.
Pero bien, la ecuación anterior tiene su origen en otra mucho más general, que es un caso particular de una recta que pasa por el origen (el o,o):
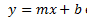
En donde b es el punto donde la recta corta al eje y, es decir, cuando x=0.
Con la formula arriba mencionada podemos construir cualquier ecuación de recta.
Vamos a intentar hallar la pendiente en este problema:
*Obtener la ecuación de una recta que pasa por los puntos A(3,5) y B(-3, 4) así como su pendiente.
Aplicando la fórmula de más arriba, tendríamos:
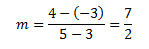
Ahora procederemos a hallar la ecuación de esta recta, sustituyendo m por su valor y b por el valor de y para x=0:
y= 7/2x +b
Como veis en este caso no podemos resolver el valor de b, ya que ninguno de estos puntos está situado en el origen, así que en principio quedaría planteada la ecuación con b, puesto que no tenemos ningún punto que sea del tipo (0,y).
Puede darse el caso de que tengamos un punto (x1,y1) y su pendiente, y necesitemos hallar su ecuación, en tal caso usamos esta fórmula:
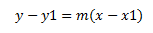
Esta es una ecuación que se utiliza cuando tenemos la pendiente y los puntos, se denomina ecuación punto-pendiente.
Para terminar me gustaría hacer hincapié en los distintos valores que puede tomar nuestra pendiente:
a) Si m<0: Es una pendiente negativa, por tanto la recta será descendente
b) Si m>0: Es una pendiente positiva, por tanto la recta será ascendente.
c) Si m=0: No hay pendiente, por tanto es una recta horizontal.
d) Si m= indefinido: Es una recta vertical, al tender su pendiente hacia el infinito, aunque estos casos seguramente no los veréis en los primeros cursos.
**Pista**: Acordaos del ejemplo de las calles, cuanto mayor es la subida, mayor será su pendiente (y viceversa), lo mismo pasa con las rectas.
