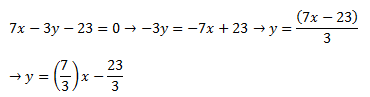Ecuación de una recta

Una recta no es más que un conjunto de puntos situados gráficamente en un plano, uno detrás de otro, guiados por un vector dirección y un vector posición.

Si representásemos una recta en el plano cartesiano, tendríamos algo así:

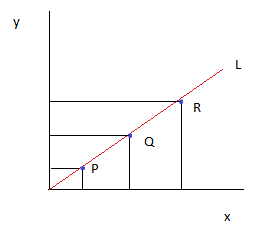
Siendo P, Q y R los puntos que conforman la recta L.

Hasta aquí todo muy fácil, pero antes hablábamos de unos vectores de dirección y posición ¿Qué serán esas cosas? Pues son unos elementos dentro de un espacio (en nuestro caso el plano cartesiano, el eje XY) que nos indican cómo se alinea nuestra recta y en qué dirección está dirigida, igual que cuando vamos en coche y vemos señales que nos indican que dirección seguir, pues es más o menos lo mismo.

Entonces, todas las rectas representadas en este plano se pueden incluir en la siguiente fórmula:

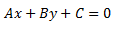
Siendo A y B distintos de cero, y conociéndose ésta ecuación como la ecuación general o implícita de la recta.

Esta ecuación parte de un desarrollo posterior, que os detallo a continuación:

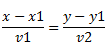
Esta es la ecuación continua de una recta, que ha de pasar obligatoriamente por el punto x1 e y1 y que tiene como vector director v=(v1, v2)

Desarrollando la ecuación de arriba nos queda(multiplicando en cruz):

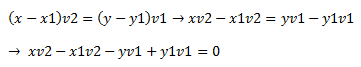
Sustituimos de la siguiente manera: A=v2, B=-v1 y C= y1v1- x1v2

Quedándonos:

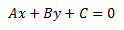
Por tanto, los componentes del vector director serán:

v= (-B,A)

Y la pendiente de la recta será:

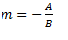
Con todo esto ya podremos hallar la ecuación de una recta que pasa por un punto. Hagamos un ejemplo:

>> Expresa las ecuaciones de esta recta de todas las maneras posibles, sabiendo que pasa por los puntos A(2, 3) y B( -1, 4):

a)Ecuación continua:

Primero necesitamos hallar el vector v, que como recordáis es v=(-B,A), por tanto, debemos cambiar de signo los componentes de B y sumarlos con los de A:

v= (-B,A)= (1,4)+(2,3)=(3,7)

Ahora con esas coordenadas, construimos la ecuación:

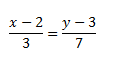
Y dejamos así.

b) Ecuación general:

Se trata de resolver la ecuación anterior, intentando poner x e ies del lado izquierdo:

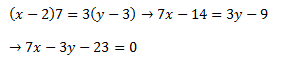
c) Ecuación explícita:

Simplemente dejamos la y del lado izquierdo sola: