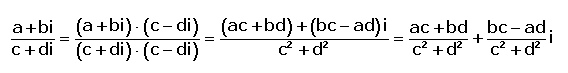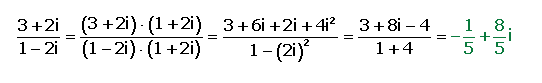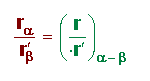Operaciones con números complejos
Ahora que ya hemos visto las diferentes formas en que se pueden presentar los números complejos, vamos a ver cómo operar con ellos. Al igual que los números reales, se pueden sumar (o restar), multiplicar y dividir; veremos que según en la forma en la que se encuentren será más o menos complicado y pesado.
OPERACIONES EN FORMA BINÓMICA
Dados dos números complejos escritos en forma binómica: z=a+bi y z´=a´+b´i, podemos definir las siguientes operaciones:
-Multiplicación de un número real k por un número complejo:
Sea k un número real, cuando multiplicamos un número complejo por una constante obtenemos un número número complejo en el que cada componente queda multiplicada por la constante: k∙z=ka+kb i.
Ejemplo: Sea z=2-3i, realiza la siguiente operación: 5∙z=5∙2-5∙3i=10-15i.
-Suma o resta de números complejos:
Cuando queremos sumar o restar dos números complejos obtenemos un nuevo número en el que la parte real es la suma o resta de las partes reales de los anteriores, y donde la parte imaginaria es la suma o resta de las partes imaginarias: z±z´= (a±c)+(b±d)i.
Ejemplo: Sean z=3+5i y z´=-2+6i, entonces: z+z´=(3+(-2))+(5+6)i=1+11i
-Producto de números complejos:
Para multiplicar dos números complejos, podemos multiplicar como si de polinomios se tratara, teniendo en cuenta que i^2=-1. O también teniendo en cuenta la siguiente fórmula:![]()
Ejemplo: Realiza el producto de los siguientes números complejos: z=5+2i, z´=2-3i.
-División de números complejos:
Para poder realizar la división de números complejos es necesario definir un nuevo concepto: sea z=a+bi, el conjugado es un número complejo con la misma parte real y cuya parte imaginaria será el opuesto: z´=a-bi.
Para realizar la división, multiplicaremos numerador y denominador por el conjugado del denominador, de tal forma que desaparece la parte compleja del denominador quedando la suma de los cuadrados de la parte real y la imaginaria:
Ejemplo: Halla el cociente de z=3+2i y z´=1-2i:
OPERACIONES EN FORMA POLAR
Recordamos que los números en forma polar vienen definidos a partir de su módulo y del argumento. Por tanto sea un número complejo z de módulo r y argumento α, y otro número z´con módulo r´y de argumento β.
Para realizar tanto el producto como la multiplicación de dos números complejos será más fácil y rápido utilizando la forma polar, como podemos ver a continuación:
-Producto de dos números complejos:
El producto de dos números complejos será un nuevo número complejo que tendrá por módulo el producto de los módulo anteriores, y como argumento la suma de los argumentos de los dos números complejos:
Ejemplo: Dados dos números complejos: z con r=6 y α=45º; y otro número z´ tal que r´=3 y β=15º, entonces:
-División de dos números complejos
La división de dos números complejos es un nuevo número complejo cuyo módulo será el cociente de los módulos anteriores y el argumento la resta de los módulos:
Ejemplo: Sea un número complejo z de módulo r=6 y α=45º; y otro número z´ tal que r´=3 y β=15º, entonces:
Por tanto, podemos concluir, que cuando tengamos que realizar sumas o restas utilizaremos la forma binómica; mientras que para realizar productos y divisiones será mucho más fácil si utilizamos el número en forma polar.