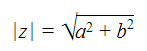Números complejos

Los números complejos surgen como solución a las raíces cuadradas negativas. Ya los matemáticos árabes e italianos trabajaron con estas raíces negativas aunque sin darle la categoría de números; fue en el siglo XVI cuando se empezaron a establecer ciertas reglas para llevar a cabo cálculos con este tipo de raíces, operando como si de números se tratara. Pero no fue hasta el siglo XVIII cuando desapareció el carácter esotérico de estas raíces y comenzaron a denotar a la raíz de -1, con al letra i. Todo esto fue debido al gran matemático Euler.

Una vez que hemos hecho algo de introducción histórica, vamos a conocer la definición, notación y propiedades de los números complejos:

DEFINICIÓN

Todo número complejo es un par de números reales (a,b), de tal forma que z=a+bi es un número complejo. Esta forma de escribir un número complejo se denomina forma binómica. El número a, se denomina parte real; mientras que b se denomina parte imaginaria.

Por tanto, podemos decir que todo número imaginario se forma mediante la suma de una parte real y otra imaginaria.

Cuando un número no tiene parte imaginaria (b=0), diremos que z es un número real. Cuando no tenga parte real (a=0), diremos que se trata de un número imaginario puro.

REPRESENTACIÓN DE UN NÚMERO COMPLEJO

Para poder llevar a cabo la representación de los números complejos, es necesario utilizar el plano, es decir, los ejes cartesianos. Estableceremos una relación (biyectiva) entre los elementos del plano y los vectores, de tal forma, que para representar el número z=a+bi, representaremos el vector (a,b), cuyo origen será el punto (0,0) y el extremo del vector será el punto P(a,b). El punto P que determina el extremo del vector se denomina afijo de z.

Gracias a la relación entre los números complejos y los vectores podemos definir dos nuevos conceptos: módulo y argumento de un número complejo:

Definición: Sea z=a+bi, se define el módulo del número complejo z como la raíz de la suma de los cuadrados de sus componentes, lo denotaremos por |z|:

Definición: Llamamos argumento θ de un número complejo z=a+bi al ángulo que forma el vector (a,b) con el de abscisas (eje OX). Teniendo en cuenta las razones trigonométricas, obtenemos que: θ=arctg b/a.

FORMA TRIGONOMÉTRICA Y POLAR DE UN NÚMERO COMPLEJO

Hemos visto al principio la forma binómica de un número complejo, pero esta no es la única, ya que dependiendo de las operaciones que tengamos que realizar o para qué lo vayamos a utilizar nos interesará pasar de una a otra.

Sea z=a+bi un número complejo en forma binómica, llamaremos r al módulo de z: r=|z|, y como ya hemos visto antes θ=arctg b/a es el argumento, entonces tenemos que: a=r∙cos θ y b= r∙sen θ . Por tanto, podemos escribir z como: z= r(cos θ+isen θ) que se conoce como la forma trigonométrica de un número complejo.

A partir de lo anterior, podemos decir, que un número complejo queda definido por su módulo (r) y su argumento ( θ), luego podemos escribir z como: , conocida como forma polar.

Como hemos visto, para pasar de forma binómica a la polar y a la trigonométrica se haría siguiendo al definición. Para pasar de trigonométrica a binómica, simplemente tendríamos que calcular el seno y coseno y operar. Y, por último, para pasar de polar a binómica, es necesario pasar por la trigonométrica.