Números naturales
Los primeros caracteres que aparecieron, y que sustituyeron a las arcaicas formas de contar con las manos o escribiendo rayas en objetos o mismamente con piedras, fueron los números, más concretamente los primeros en destacar por ser más sencillos y fáciles de hallar fueron los números naturales.
Los números naturales son aquellos que utilizamos principalmente para contar, es decir, los que son positivos y sin parte decimal alguna. En este grupo se excluyen los números negativos, fraccionarios e irracionales.
Expresado matemáticamente, los números naturales estarían contenidos en un conjunto N:
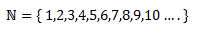
Como veis el cero no está contenido en el grupo de los números naturales, eso ya os lo aclararé más adelante cuando hable de las propiedades.
Dicho conjunto contiene clases simbolizadas por cifras, que representan el número de elementos que contiene esa cifra, por ejemplo, 5, significa que está formado por 5 elementos.
Tienen dos utilidades básicas ordenar los elementos de un conjunto(ordinales) y para contar los elementos de ese conjunto(cardinales).
Con este números podemos realizar las operaciones básicas de sumar y multiplicar, y el resultado de éstas será siempre un número natural. No ocurre así con la resta, pues puede darse el caso que el resultado sea negativo (el minuendo sea menos que sustraendo), y puesto que antes dijimos que no existían números naturales negativos, consideramos que no se trata de una operación natural (o interna).
Para terminar de aclarar lo que son los números naturales, me gustaría que observaseis este postulado (o axioma) en donde se intenta explicar la estructura de los números naturales:
1. El 1 es un número natural.
2. Si n es un número natural, entonces el sucesor de n también es un número natural.
3. El 1 no es el sucesor de ningún número natural.
4. Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
5. Si el 1 pertenece a un conjunto, y dado un número natural cualquiera, el sucesor de ese número también pertenece a ese conjunto, entonces todos los números naturales pertenecen a ese conjunto.
**Pista**: el sucesor se refiera al número siguiente, por ejemplo, el sucesor del 2 es el 3. Por eso el 1 no es sucesor de ningún número natural, pues digamos que es la medida mínima dentro del conjunto.
Además de las operaciones básicas de suma y multiplicación, los números naturales también son fundamentales en otras áreas de las matemáticas y la ciencia. Por ejemplo, en la teoría de conjuntos, los números naturales se utilizan para definir el tamaño (o cardinalidad) de conjuntos finitos. También son esenciales en la teoría de números, donde se estudian las propiedades y relaciones de los números enteros.
En la educación matemática, los números naturales son uno de los primeros conceptos que se enseñan a los niños. Aprender a contar, sumar y multiplicar con números naturales sienta las bases para el aprendizaje de conceptos matemáticos más avanzados. Los juegos y actividades que involucran la manipulación de objetos físicos, como bloques o fichas, son métodos comunes para enseñar a los niños sobre los números naturales.
Históricamente, la comprensión y el uso de los números naturales han evolucionado significativamente. Las antiguas civilizaciones, como los babilonios y los egipcios, ya utilizaban sistemas numéricos para llevar registros y realizar cálculos. Sin embargo, fue en la antigua Grecia donde los matemáticos comenzaron a desarrollar una teoría más formal de los números. Euclides, por ejemplo, en su obra «Elementos», presentó una serie de proposiciones y teoremas que forman la base de la teoría de números.
En la actualidad, los números naturales siguen siendo un área activa de investigación. Los matemáticos continúan explorando nuevas propiedades y relaciones entre estos números, así como sus aplicaciones en otras disciplinas. Por ejemplo, en informática, los números naturales se utilizan en algoritmos y estructuras de datos, y en física, se emplean para describir cantidades discretas y fenómenos cuantizados.
Finalmente, es importante mencionar que existen diferentes notaciones y convenciones para los números naturales en distintas culturas y contextos. Aunque en la mayoría de los casos se utiliza el sistema decimal, también existen otros sistemas de numeración, como el binario y el hexadecimal, que son especialmente relevantes en el campo de la informática.
