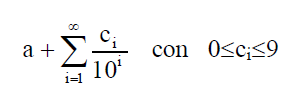Números decimales

El conjunto de los números decimales está formado por todos los números reales que se pueden escribir de la siguiente manera a,c1c2c3…..

Es decir, son aquellos números que poseen una parte decimal, que es la parte que va detrás de la coma: c1c2c3c4… La parte que está delante de la coma, a, se denomina parte entera.

Para leerlos se suelen utilizar las siguientes formas:

– Dos coma 5.

– Dos con 5.

– Dos unidades y 5 décimas.

NOTACIÓN DECIMAL

Aunque la forma correcta matemáticamente para expresar un número decimal es la que hemos mencionado al principio (con una coma) también podemos hallar números decimales escritos de la siguiente manera:

-Con un punto: en lugar de poner una coma para separar la parte entera de la decimal, podemos poner un punto: a.c1c2c3c4…, de esta forma es como suele expresarse en ordenadores y calculadoras.

-Con un apóstrofo: en lugar de la coma o el punto: a´c1c2c3….

CLASIFICACIÓN DE LOS NÚMEROS DECIMALES

Los números decimales se pueden en clasificar en tres grupos: exactos, periódicos y mixtos.

-Decimales exactos: Son los números que tienen un número finito de decimales. Podemos escribirlos como una fracción cuyo denominador está formado por potencias de 10 (dependiendo del número de decimales), y el denominador es el número sin decimales. Por tanto pertenecen al subconjunto de los números racionales.

Ejemplos: a) 2,34=234/100 b) 0,345=345/1000

-Decimal periódico: Son los números decimales cuya parte decimal es infinita, pero esta se repite siguiendo un mismo patrón, denominado periodo. Para poder representar la parte periódica se escriben los números que la forman y encima se coloca un arco o “gorrito”:

También pueden escribirse en forma de fracción, por tanto también pertenecen al subconjunto de los números racionales.

Dentro de los decimales periódicos vamos a distinguir dos tipos: los decimales periódicos puros y los decimales periódicos mixtos.

Decimal periódico puro: Son aquellos cuya parte decimal está formada por el periodo de forma íntegra, es decir, justo después de la coma todos los números se repiten periódicamente, como el ejemplo anterior.

Para escribirlo en forma de fracción escribimos en el numerador la diferencia entre el número decimal sin coma (y evidentemente sólo con el periodo una) y la parte entera; y en el denominador escribiremos tantos nueves como de cifras conste el periodo, es decir, si el periodo está formado por dos números el denominador será 99.

Ejemplo: 2,3737373737373=(237-2)/99=235/99

Decimal periódico mixto: Son los números cuyo parte decimal está forma por una parte que no se repite (que se encuentra justo después de la coma) y una parte que se repite que llamamos periodo y denotamos de la misma manera que en el caso anterior, con el “gorrito”:

Para escribirlo en forma de fracción escribimos en el numerador la diferencia entre el número sin coma (igual que en el caso anterior) y la parte entera seguida de la parte decimal no periódica (sin coma, por supuesto); y en el denominador tantos nuevos como cifras tenga la parte periódica (igual que en el caso anterior) seguidos de tantos ceros como cifras tenga la parte decimal no periódica.

Ejemplo: 5,678888888=(5678-567)/900=5111/900

-Decimal no periódico: Estos números como su nombre indica no pueden expresarse utilizando un periodo, porque la parte decimal es infinita y no sigue ningún patrón. Por tanto, no pueden ser representados por medio de fracciones y corresponden al conjunto de los números irracionales. Muchos de estos números irracionales se expresan mediante símbolos, los más famosos son por ejemplo, el número e o el número pi (π).

USO DE LOS NÚMEROS DECIMALES

Los números decimales tienen una amplia variedad de aplicaciones en la vida cotidiana y en diversas disciplinas científicas. En la vida cotidiana, se utilizan para representar cantidades que no son enteras, como el precio de un artículo, la longitud de un objeto, la capacidad de un recipiente, entre otros.

En ciencias como la física y la química, los números decimales se utilizan para representar cantidades que son demasiado pequeñas o demasiado grandes para ser representadas de manera conveniente con números enteros. Por ejemplo, la masa de un átomo se expresa en unidades de masa atómica, que son una fracción muy pequeña de un gramo.

En matemáticas, los números decimales son fundamentales en el estudio de las propiedades de los números reales. Por ejemplo, se utilizan para definir la noción de límite, que es fundamental en el cálculo.

Además, los números decimales también son esenciales en la informática. Los ordenadores utilizan una representación binaria de los números decimales para realizar cálculos. Esta representación se basa en la idea de que cualquier número decimal puede ser expresado como una suma de fracciones cuyos denominadores son potencias de 2.

En resumen, los números decimales son una herramienta fundamental en una amplia gama de disciplinas y aplicaciones. Su estudio y comprensión son esenciales para cualquier persona que desee tener una comprensión sólida de las matemáticas y las ciencias.