Octoniones

Fueron descubiertos por John T. Graves en 1843, quien fue amigo de William Hamilton quien los llamó octavas. Independientemente fueron descubiertos por Arthur Cayley, quien lo publicó por primera vez en 1845, por lo cual a veces son llamados números de Cayley o álgebra de Cayley.

Los octoniones son la extensión no asociativa de los cuaterniones. Los cuaterniones o cuaternios son una extensión de los números reales, semejante a la de los números complejos. Mientras que los números complejos son una extensión de los reales por la adición de la unidad imaginaria i, tal que,

Los cuaterniones son una extensión generada de manera a partir de la adición de las unidades imaginarias: i, j y k a los números reales, tal que,

Ya que los octoniones consisten en dos cuaterniones, forman un espacio de vector dimensional 8 sobre los números reales y pueden pensarse como un octeto ordenado de números reales. Cada octonión forma y representa una combinación lineal de la base: 1, e1, e2, e3, e4, e5, e6, e7. La adición de octoniones se realiza con la suma de los coeficientes correspondientes, como son los números complejos y los cuaterniones. La forma de multiplicar octoniones se puede determinar con la tabla de multiplicación que vemos a continuación:

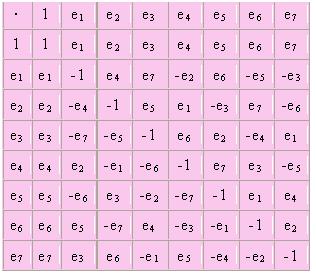
Este producto no es conmutativo ni asociativo. Por razón de esta no asociatividad, los octoniones, a diferencia de los cuaterniones, no admiten una representación matricial.

En física los Octoniones se utilizan para la generalización no asociativa de los mecanismos del quántum. Por ejemplo, la ecuación de Heisenberg del movimiento se modifica usando un conmutador no asociativo. También se utilizan en temas como la teoría de la secuencia y la relatividad especial.