Cuaterniones

Los cuaterniones son miembros de un cuerpo no conmutativo inventado por primera vez por William Rowan Hamilton .A pesar de no ser conmutativos sí son asociativos. Se puede decir que son una extensión de los números reales, equivalente a la de los números complejos, estos en cambio son una extensión de los número reales por la adición de la unidad imaginaria i, tal que i al cuadrado sea igual a -1. Los cuaterniones son entonces una extensión que se genera de forma análoga añadiendo las unidades imaginarias:

Esto se puede abreviar como se muestra en la siguiente tabla de multiplicación:

Llamamos cuaternión a un número de la forma a + bi + cj + dk, donde a, b, c, y d son números reales que se determinan por cada cuaternión. Los cuaterniones pueden tener diversas representaciones. Por la semejanza con los números complejos, se pueden representar como la suma de una parte real y una imaginaria, que podría ser:

Siendo a, b, c y d números reales

En forma matricial la representación puede ser la siguiente:

Aquí z y w son números complejos, a, b, c y d son reales y Ż es el complejo conjugado de z.

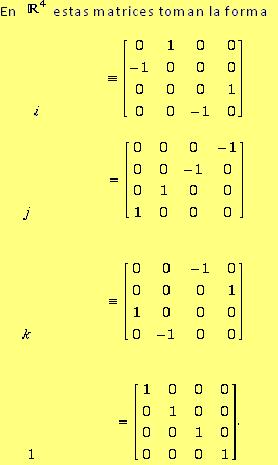
Como forma matricial alternativa tenemos la que maneja como bases las matrices 2×2, siendo los cuaterniones combinaciones lineales de estas:

De modo que I, J y K son las tres soluciones de la ecuación matricial:

Cumpliéndose las igualdades siguientes:

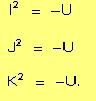
Por lo tanto, I, J y K se pueden considerar raíces negativas de la matriz unidad. Denominamos A la combinación lineal de estas cuatro matrices con coeficientes enteros, entero hamiltoniano.

La última representación sería la más simple y cómoda a la hora de operar, también se constituye por una parte real, w, y una imaginaria, (x, y, z), pero a diferencia de la anterior, la parte imaginaria se agrupa junto a un vector, v, de modo que la representación resultante sería:

q= [v, w]

Por razón de esta representación podemos identificar los números reales con los cuaterniones de la forma q = [0,s] , y los vectores de R al cubo con los de la forma :

q = [v, 0].

Los cuaterniniones se utilizan utilizados en los gráficos por ordenador como coordenadas para las rotaciones y orientaciones. Su facilidad de uso permite que compita con las coordenadas más tradicionales, como lo son las matrices o los ángulos de Euler. Aunque posiblemente sean la forma más sofisticada y práctica de tratar coordenadas homogéneas en el espacio tetradimensional se ignoran en los programas de la mayoría de las universidades.