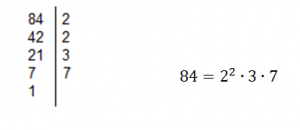Números primos
Vamos a indagar un poco más en la Teoría de Números presentando un nuevo concepto que a la vez es muy conocido por todos: los números primos.
No conocemos a ciencia cierta el año exacto en qué aparecieron los números primos, pero ya hace más de 20000 años (que se dice pronto) parece ser que trabajaban con ellos o por lo menos los conocían, debido a las marcas encontradas en un hueso. Aunque las primeras pruebas escritas datan del 300 a.C. en la famosa obra “Los Elementos de Euclides”, donde se da una definición de los números primos y demuestra que existen infinitos.
Definición: Diremos que un número natural, p distinto de 0 y 1; es un número primo, si los únicos divisores de p son el 1 y él mismo. Los números que no son primos reciben el nombre de números compuestos.
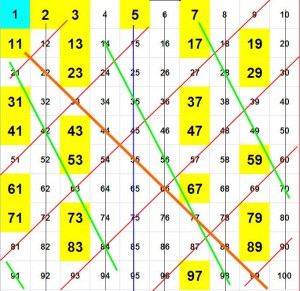
De tal forma podemos concluir que el primer número primo es el 2, el siguiente el 3, el 4 sería un número compuesto, puesto que es divisible por 2; el 5 es primo… y, ¿hasta dónde podríamos continuar? Este proceso es infinito y a lo largo de la historia ha sido estudio de muchos sabios y científicos. El primer método conocido es la Criba de Eratóstenes; este proceso permite conocer los números primos hasta un número dado. Consiste en elaborar una tabla en la que aparezcan todos los números y a partir de ella procederemos de la siguiente forma:
1º) Seleccionamos el primer número primo que nos encontramos, el 2, y tachamos todos los múltiplos de este.
2º) Seleccionamos el siguiente número primo (el siguiente número que quede sin tachar), el 3, y tachamos todos los múltiplos de 3. Y así sucesivamente.
De tal forma que la Criba de Eratóstenes para los 100 primeros números queda de la siguiente manera:
Los números coloreados en amarillo, serían los números primos hasta el número 100. Recordad que el número 1 no se considera un número primo por convencionalismo.
Como podemos ver, este proceso resulta demasiado pesado conforme n se hace cada vez más grande. Por esa razón se ha ido perfeccionando este método por medio de algoritmos, y ahora se puede decir, que es un ordenador el que busca los números primos.
PROPIEDADES DE LOS NÚMEROS PRIMOS
1. Si p y q son números primos y p|q, entonces p y q son asociados: p = 1•q=(-1)•q.
2. Si p es primo y p|a, entonces M.C.D. (p,a)=p.
3. Si p es primo y p|ab, entonces p|a o p|b.
DESCOMPOSICIÓN FACTORIAL DE UN NÚMERO
Por último vamos a ver una de las aplicaciones más importantes de los números primos, la descomposición factorial de un número, ya que cualquier número compuesto ( el que no es primo) puede ser factorizado de forma única, sin tener en cuenta el orden, en producto de números primos: n= p1•p2•………..•pn
Ejemplo: Descomponer el número 84 en números primos:
Este proceso se utiliza sobre todo para hallar el máximo común divisor (MCD) y el mínimo común múltiplo (mcm).