Número factorial

Si tenemos por ejemplo un número n, que represente un número natural mayor que 1, lo llamaremos factorial de n y lo representaremos como n!, al producto de los n número no nulos que aparecen primero. Con esto lo que queremos decir es que un número factorial es el producto de varios números naturales siguientes a partir de uno. Entonces para todo número natural n, se denomina factorial o factorial de n al producto de todos los números naturales desde 1 hasta n. Observemos el siguiente ejemplo:

Si consideramos que todos los productos poseen al menos dos factores, no tendría sentido el uso de las cifras 0 y 1. Pero para qué sea posible aplicar las fórmulas a todos los casos, definiremos los números factoriales de 0 y 1 como 0!=1 para que la relación n!=n. (n-1) sea válida también para n=1. Tengamos en cuenta también que 1!=1

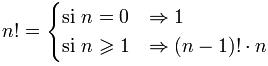
El matemático francés Christian Kramp fue quien popularizó la notación n!

Si queremos averiguar un número factorial, podemos proceder de la siguiente forma. Siendo n un número natural, llamaremos factorial de n y lo notaremos como n! al producto de n por cada uno de los naturales que sean menores a él.

n!=n(n-1)(n-2)…..3 2 1

1!=1

0!=1 (por definición).

Aquí tenemos un ejemplo:

5! (factorial de 5) = 1 * 2 * 3 * 4 * 5 (Multiplicamos)=120

Producto de los primeros 5 números naturales.

Podemos también multiplicar al revés:

5*4=20*3=60*2=120*1=120

Las propiedades de los números factoriales son las siguientes:

* Si multiplicamos n factorial por n + 1 obtendremos como resultado n + 1 factorial, o sea que, n! (n + 1)= (n + 1)! Es posible también de esta propiedad deducir que si dividimos el factorial de n + 1 entre n factorial lograremos obtener n + 1,

O sea que (n + 1)! / n! = n + 1

* Si multiplicamos por otra parte un número factorial k! por sus números consecutivos hasta alcanzar a n obtendremos el factorial de n.

Los números factoriales generalizados son productos de factores próximos en orden inverso. Siendo n y k dos números naturales mayores que 1 y siendo n mayor o igual que k, lo denominamos factorial generalizado de n de orden k, y se simboliza como n(k) al producto de k factores descendientes a partir de n.

Tal cual pasa en el caso de los factoriales, los símbolos n(0) y n(1) carecen de sentido, pero para que sea posible el uso de las fórmulas, se constituye que n(0) = 1 y n(k) = n

Las factoriales se utilizan considerablemente en la rama de la matemática combinatoria. Por medio de esta, las factoriales intervienen en el cálculo de las probabilidades así como también en el ámbito del análisis