Momento de un vector

Un vector es un segmento orientado en el espacio el cual se caracteriza por cuatro elementos como son, el punto de origen, la dirección o línea de acción, que sería la línea que contiene al vector, el sentido del vector y el módulo del vector que es su longitud. Los vectores pueden clasificarse en libres, los cuales no se consideran asociados a ningún punto ni recta particular.

Los vectores ligados, que se asocian a un determinado punto en el espacio, que llamamos punto de aplicación y los vectores deslizantes que pueden considerare en cualquier posición dentro de una recta. Dos vectores de igual módulo y sentido sobre la misma recta, son el mismo vector deslizante. Dependiendo la circunstancia se puede convenir considerar el vector libre de igual módulo y dirección que un vector ligado o deslizante. Decimos entonces que se trata del vector libre asociado al vector ligado o deslizante. Llamamos a dos vectores, equipolentes si poseen el mismo vector libre asociado.

Las operaciones más comunes con vectores son la Adición de vectores, producto de un vector por un escalar, producto escalar de dos vectores y producto vectorial de dos vectores. Es necesario tener presente la definición de estas operaciones para poder para poder abordar el tema “momento de un vector”. Las operaciones nombradas se definen para vectores libres, aunque también pueden definirse para vectores deslizantes o ligados dependiendo de la circunstancia. Por ejemplo, la adición de vectores deslizantes se define si las rectas de acción de los vectores pasan por un punto. Decimos que sistema de vectores es un conjunto de vectores del mismo tipo. Por lo cual, hay sistemas de vectores ligados, deslizantes y libres. En álgebra vectorial y física se denomina momento de un vector a una magnitud que establece una relación entre uno o varios vectores y una recta, un plano o un punto.

El momento de un vector respecto de un punto se define como el producto vectorial del vector de posición del origen del vector respecto de O por el propio vector. Haremos referencia ahora al momento de un par de vectores respecto de un punto.

Se llama par de vectores al conjunto que está formado por dos vectores que poseen el mismo módulo, la misma dirección y sentidos contrarios. El resultado de la suma de ambos es el vector nulo.

El momento de un vector con respecto a un eje, se define como la proyección sobre dicho eje del momento de ese vector respecto a un punto del eje. El momento es independiente del punto elegido sobre el eje. Veamos ahora detalladamente el momento de un vector deslizante v respecto de un punto O.

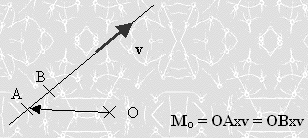
En la figura podemos ver un vector Mo que normalmente se considera ligado al punto O, aunque también e puede considerar libre. Siendo A un punto cualquiera de la recta de acción, su valor se conoce a partir del producto vectorial OAxv. El resultado será independiente del punto elegido sobre la recta de acción.

Momento de un vector deslizante respecto de una recta (r).

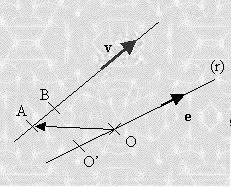
M(r) = (Mo.e)e = ((OAxv).e)e = ((O»Bxv).e)e = …

Este es un vector deslizante sobre la recta. Se obtiene proyectando sobre la recta el momento respecto a uno de sus puntos O, por lo cual es indiferente el punto O que se elija sobre la recta. Si es e corresponde a un vector unitario sobre la recta, el valor del momento respecto de la recta viene dado por (Mo.e)e.

Una propiedad que podemos nombrar a partir de esto sería que los momentos respecto de tres rectas que sean coincidentes con unos ejes coordenados cartesianos, son las componentes vectoriales del momento respecto del origen de coordenadas. Veamos:

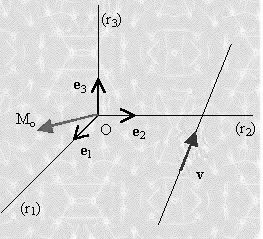
Mo = M(r1) + M(r2) + M(r3)

El momento puede considerarse un vector ligado al punto respecto del que se calcula, o bien como un vector libre. La primera podría ser la mas natural, ya que el momento de un vector o sistema es función del punto. Podemos decir coloquialmente que existe una forma de ligadura entre el momento y el punto de cálculo. Esto no implica necesidad de considerar el vector momento como ligado al punto.