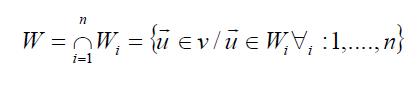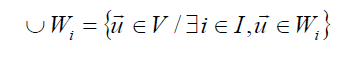Espacios vectoriales

Como ya vimos en un post anterior, un espacio vectorial en una estructura algebraica formada por un conjunto no vacío V sobre el que se define una operación interna (V,+) entre elementos de V, llamada suma; y una operación externa ● sobre K, llamada producto por un escalar por un escalar.

Hoy nos vamos a centrar en las propiedades y operaciones concretas que se dan en los espacios vectoriales.

Definición:Llamamos vectores a los elementos del espacio vectorial, mientras que los elementos del cuerpo K reciben el nombre de escalares.

OPERACIONES EN EL ESPACIO VECTORIAL

-Suma de vectores: Dados dos vectores u=(u1,u2) y v=(v1,v2); se define la suma de u+v como un nuevo vector cuya primera coordenada viene dada por la suma de las primeras coordenadas de u y v, y cuya segunda coordenada será por tanto la suma de las segundas: u+v=(u1+v1,v2+v2)

-Producto de un escalar por un vector: Dado un vector u=(u1,u2) y un escalar a; se define el producto de un escalar por un vector, como un nuevo vector, cuyas coordenadas vienen dadas por la multiplicación del escalar por cada una de ellas: au=(au1,au2)

PROPIEDADES.

Para todo para de vectores u,v de V; y para todo para de escalares a y b, se cumplen:

1. 0u=0, donde el primer cero es un escalar y el resultado es un vector.

2. Análogamente, a0=0, en este caso, tanto el primer cero como el último son vectores.

3. (-a)u=a(-u)=-au

4. La propiedad distributiva para la diferencia respecto a vectores: a(u-v)=au-av

5. La propiedad distributiva para la diferencia respecto a escalares: (a-b)u=au-bu

6. Si au=0, entonces a=0 o u=0.

SUBESPACIO VECTORIAL

Definición: Dado un espacio vectorial V, y WcV un subconjunto no vació de V, diremos que W es un subespacio vectorial de V si cumple las siguientes condiciones:

a) Dados w1 y w2, dos vectores de W, la suma tiene que ser un elemento de W, es decir, w1+w2 ɛ W. O lo que es lo mismo que (W,+) sea un subgrupo de (V,+).

b) Dado un escalar a, y un vector de W, w, entonces: el producto, aw, tiene que estar en W.

OPERACIONES ENTRE SUBESPACIOS

-Intersección de subespacios: Dada la familia de subespacios Wi de un espacio vectorial V, la intersección de subespacios es un nuevo subespacio vectorial, de tal forma que si un vector está en la intersección, quiere decir que está en todos los subespacios de la familia.

-Unión de subespacios: Dada una familia de subespacios Wi de un espacio vectorial V, como el conjunto formado por los vectores de todos los Wi:

No se cumple en todos los casos que la unión de subespacios vectoriales sea un subespacio vectorial.

-Suma de subespacios: En las condiciones anteriores, definimos la suma de subespacios, como el subespacio de V formado por los vectores que se obtienen al sumar vectores de Wi:

-Suma directa de subespacios: Sean W1 y W2 dos subespacios del espacio vectorial V. Diremos que W es suma directa de W1 y W2 si:

1. W1+W2=W

2. Y la intersección de W1 y W2 es el vector nulo: W1 ∩ W2 = {0}

La suma directa se presenta de la siguiente forma: