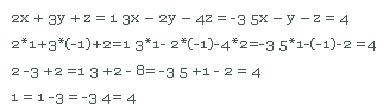Método de Gauss-Jordan

Este método debe su nombre a Carl Friedrich Gauss y a Wilhelm jordan. Se trata de una serie de algoritmos del algebra lineal para determinar los resultados de un sistema de ecuaciones lineales y así hallar matrices e inversas. El sistema de Gauss se utiliza para resolver un sistema de ecuaciones y obtener las soluciones por medio de la reducción del sistema dado a otro que sea equivalente en el cual cada una de las ecuaciones tendrá una incógnita menos que la anterior. La matriz que resulta de este proceso lleva el nombre que se conoce como forma escalonada.

Este método, permite resolver hasta 20 ecuaciones simultáneas. Lo que lo diferencia del método Gaussiano es que cuando es eliminada una incógnita, se eliminará de todas las ecuaciones restantes, o sea, las que anteceden a la ecuación principal así como de las que la siguen a continuación. De esta manera el paso de eliminación forma una matriz identidad en vez de una matriz triangular. No es necesario entonces utilizar la sustitución hacia atrás para conseguir la solución.

Para resolver sistemas de ecuaciones lineales con el método Gauss Jordan, debemos en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales con la notación matricial, por ejemplo:

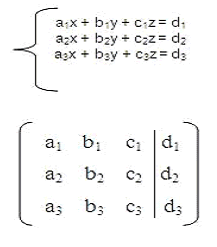
También se le llama matriz aumentada.

Luego de realizado lo anterior procederemos a transformar dicha matriz en una matriz identidad, o sea una matriz equivalente a la inicial, de la forma:

Logramos esto aplicando a las distintas columnas y filas de las matrices, restas, sumas, multiplicaciones y divisiones. Debemos tener en cuenta que las operaciones utilizadas se aplicarán en todos los elementos de la fila.

En dicha matriz identidad no vemos los términos independientes. Esto sucede ya que cuando la matriz original alcance la matriz identidad, los términos serán la solución del sistema y verificarán la igualdad para cada variable que se corresponderán de la forma siguiente:

• d1 = x

• d2 = y

• d3 = z

Ahora teniendo clara esta base, analicemos detalladamente este método con un ejemplo concreto.

Sea el siguiente sistema de ecuaciones:

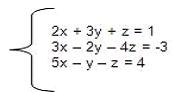
Aplicaremos luego el primer paso, o sea que lo anotaremos en forma matricial:

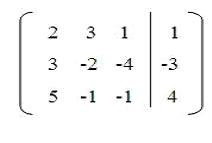
Realizado lo anterior, podemos operar con las distintas columnas y filas de la matriz para así convertirla en la matriz identidad, sin olvidar la forma del sistema:

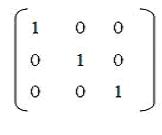
Ahora debemos transformar el 2 de la primera fila de la matriz original en el 1 de la primera fila de matriz identidad. Para realizar este paso multiplicamos toda la fila 1 por el inverso de 2, o sea ½. Veamos como nos queda:

A continuación debemos obtener los dos ceros de la primera columna de la matriz identidad. Para lograrlo buscaremos el opuesto de los números que se encuentren por debajo del 1 de la primera columna. El opuesto de 3 será -3 y el de 5 -5. Hecho esto multiplicaremos los opuestos de estos números por cada uno de los elementos de la fila primera y estos se adicionarán a los números de sus respectivas columnas Por ejemplo en el caso de la segunda fila, se multiplicará a -3 que es el opuesto de 3, por cada uno de los elementos de la primera fila y se añadirá el resultado con el número correspondiente de la columna de la segunda fila. Veamos el ejemplo:

A medida que realicemos este procedimiento operando con las distintas filas y columnas de la matriz, observaremos como esta se transforma en el modelo de la matriz identidad. Finalizado el proceso, encontraremos finalmente en la cuarta columna los valores de las variables. Veamos entonces como nos quedaría:

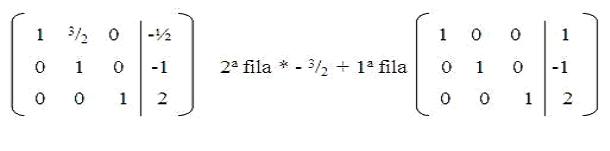
x= 1

y= -1

z= 2

Resuelto el sistema de ecuaciones, podemos verificar como último paso: