Común denominador

El método del denominador común se utiliza para la obtención de fracciones equivalentes que posean el mismo denominador(por eso lo de común, el mismo).

 

Para poder realizar este paso, debes conocer como hallar el mínimo común múltiplo. ¿Qué no sabes? Pues….vaya problema. Pero ya que estamos también lo explicamos aquí, que nada nos cuesta ¿No? Vamos por partes, como dijo Jack el destripador:

 

-El mínimo común múltiplo de dos o más número es aquel múltiplo que es menor y distinto de cero. Ya, que te hablo en chino, si no pasa nada, aquí no comemos a nadie. Aquí e dejo un ejemplo:

Supongamos 3 números, 15, 27 y 81, para saber sus múltiplos (los factores, las potencias que forman esos números) tendremos que factorizarlos (descomponerlos):

 

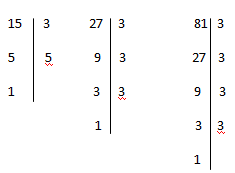
Como veis hemos descompuesto los tres números en potencias, dividiéndolos una y otra vez hasta que no pudimos más, quedándonos, una vez factorizados esos números , así:

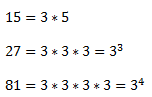
Los factores pues, son 3 y 5 y elevados a sus mayores exponentes tenemos: 3^4 y 5. Ahora hemos de multiplicar esos factores cuyo exponente es el más grande:

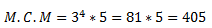
**Pista** : Para decirlo más simple, después de realizada la descomposición de los números, cogéis los factores obtenidos que tengan el mayor exponente, aunque solo aparezcan una sola vez, como el 5.

 

Bueno, ahora que ya sabemos como hallar el m.c.m, procedemos a hallar el común denominador, en este caso escogeremos dos fracciones 3/4 y 8/3, las cuales no son equivalentes entre sí:

1º) Calculamos el m.c.m de los divisores, es decir, de 4 y 8 :

4 = 2^2

3= 3

Por tanto, el m.c.m es 2^2*3, es decir, 12. Ahora ponemos ambas fracciones bajo el mismo denominador, pero sus numeradores van a sufrir un cambio.

2º) Para procederá calcular numeradores, efectuamos esta fórmulaà Numerador nuevo = numerador antiguo * (M.C.M / denominador antiguo).

Si lo aplicamos al ejemplo de antes (3/4 y 8/3) :

Numerador nuevo = 3* (12/4) = 3*3 =9

Numerador nuevo(2) = 8*(12/3) = 8*4 =32

3º) Ponemos las nuevas fracciones resultantes con sus denominadores comunes:

 

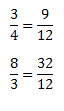
Esto puede no pareceros muy útil ahora mismo, pero pensad, por ejemplo, en la suma de fracciones, sino hiciésemos este paso, sería muy complicado calcular la suma entre 3/4 y 8/3 por ejemplo, ya que ahora mismo sería solamente sumar sus numeradores como si una suma corriente se tratase.

 

Además, es importante mencionar que el método del denominador común no solo se aplica a la suma de fracciones, sino también a la resta. Imagina que tienes que restar 5/6 y 2/9. Primero, hallamos el m.c.m de 6 y 9:

6 = 2 * 3

9 = 3^2

El m.c.m es 2 * 3^2 = 18.

Ahora, convertimos ambas fracciones al mismo denominador:

Numerador nuevo = 5 * (18/6) = 5 * 3 = 15

Numerador nuevo(2) = 2 * (18/9) = 2 * 2 = 4

Las fracciones equivalentes son 15/18 y 4/18. Ahora es mucho más sencillo realizar la resta: 15/18 – 4/18 = 11/18.

Otro aspecto interesante es que este método también se puede aplicar en problemas más avanzados de álgebra, donde se trabaja con fracciones algebraicas. Por ejemplo, si tienes que sumar (x/2) + (3x/4), primero encuentras el m.c.m de 2 y 4, que es 4. Luego, conviertes las fracciones a un denominador común:

Numerador nuevo = x * (4/2) = x * 2 = 2x

Numerador nuevo(2) = 3x * (4/4) = 3x

Las fracciones equivalentes son (2x/4) y (3x/4). Ahora puedes sumarlas fácilmente: (2x/4) + (3x/4) = (5x/4).

Finalmente, recuerda que el dominio de estos métodos no solo facilita la resolución de problemas matemáticos en el aula, sino que también es una habilidad útil en la vida cotidiana. Desde dividir una receta hasta ajustar proporciones en proyectos de bricolaje, el conocimiento de cómo encontrar un denominador común puede ser muy práctico.

Y eso es todo, recordad que podéis consultar lo referente a factorización más detalladamente aquí también, en laguia200, en este mismo blog.