Simplificación de fracciones algebraicas

En matemática diremos que la simplificación o reducción de fracciones es la acción de dividirse el numerador y el denominador de una fracción por otro mismo número con el fin de obtener otra fracción equivalente, cuyo cociente tenga el mismo valor numérico.

Podemos decir que una fracción está reducida a sus términos más simples o completamente simplificados cuando no existe ningún factor común al numerador y el denominador.

Indudablemente una fracción dada puede reducirse a sus términos más sencillos si se divide el numerador y el denominador entre los factores que tengan estos en común. Podemos llamar entonces a este proceso cancelación de factores comunes, observemos el siguiente ejemplo :

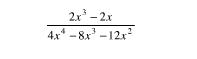
Para obtener la solución de este ejercicio en primer lugar factorizaremos el numerador y el denominador y seguido a esto procederemos a cancelar los factores comunes a ellos:

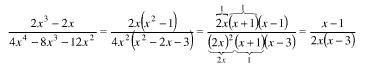
Para simplificar o reducir una fracción algebraica a una expresión algebraica entera o mixta, procederemos a dividir el numerador entre el denominador. En caso de que la división sea exacta, la fracción equivalente será una expresión algebraica entera. En caso de que la división no sea exacta se proseguirá con la división hasta que el término del resto sea de un grado menor que el primer término perteneciente al divisor y al cociente de esta forma obtenido, se le añadirá una fracción en la cual el numerador sea el resto cuyo denominador sea el divisor.

En el siguiente ejemplo reduciremos la siguiente fracción algebraica a una expresión algebraica entera, para su solución dividiremos el numerador entre el denominador:

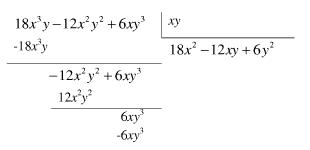
Entonces:

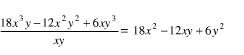
En el siguiente ejemplo reduciremos a expresión algebraica mixta una fracción algebraica, para su solución dividiremos el numerador entre el denominador, el resultado de la división no será exacto:

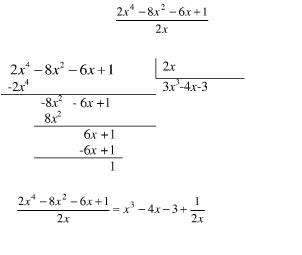
En caso de reducir una expresión algebraica mixta a una fracción algebraica, se tendrá que multiplicar la parte entera por la parte del denominador y el producto resultante se le suma luego algebraicamente al numerador. De esta forma el resultado que obtenemos es el numerador de la fracción algebraica, mientras el denominador de la fracción algebraica será el mismo que el de la expresión algebraica mixta:

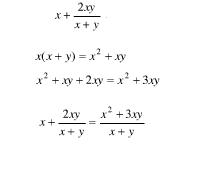
Una fracción es irreducible cuando su numerador y denominador no tienen más factores divisores comunes que los de la unidad. Por ejemplo 3x/7x no es una fracción que no sea pueda reducir ya que tiene a “x” como factor común del numerador y denominador es un divisor de ambos. Si eliminamos x por división tendremos como resultado 3/7, que en este caso es irreducible. En caso de querer encontrar de una fracción dada la fracción irreducible, debemos descomponer en factores su numerador y denominador. Luego de esto dividir cada término por cada factor común.

Podemos también realizar simplificaciones de fracciones en las cuales sus términos tengan factores monomios comunes. Veamos el siguiente ejemplo:

Se pueden realizar también reducciones de fracciones cuyos términos tengan factores binómicos:

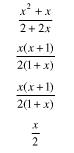
Observemos también este ejemplo en donde la simplificación de fracciones se realiza en aquellas cuyos términos tienen factores binómicos opuestos:

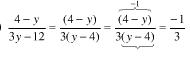
Vemos aquí fracciones con trinomios:

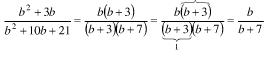
Para simplificar fracciones algebraicas al mínimo común denominador debemos transformarlas en fracciones equivalentes, que posean el menor denominador que sea posible. Entonces para reducir fracciones algebraicas al mínimo común denominador primero simplificaremos al máximo las fracciones que tenemos dadas, como siguiente paso hallaremos el mínimo común múltiplo de los denominadores, los cuales serán el mínimo común denominador de las fracciones equivalentes. Para hallar luego los numeradores de las fracciones que sean equivalentes dividiremos al mínimo común denominador que obtuvimos anteriormente entre cada uno de los denominadores, para luego multiplicar los cocientes naturales por cada uno de los numeradores respectivos.