Matrices de Pauli
Las matrices de Pauli, se denominan de tal forma en honor al físico austríaco Wolfgang Ernst Pauli. Se puede decir que Pauli es uno de los fundadores de la mecánica cuántica. Las matrices que llevan su nombre son utilizadas en física cuántica dentro de la manifestación del momento angular intrínseco, también denominado espín. Habitualmente son indicadas con la letra griega “sigma” (σ). Cuando se les indica con la letra “tau” (τ) es por que hay una relación con el isospin (espín isotópico o espín isobárico).
En la ciencias matemáticas las matrices de Pauli forman una base vectorial correspondiente al álgebra de Lie (es una estructura en álgebra que representa a un grupo de transformaciones o alternativas infinitesimales) que pertenece al llamado grupo especial unitario SU(2), el cual actúa relacionandose con el carácter de segunda dimensión. El grupo especial unitario de grado n corresponde a una agrupación de de matrices unitarias n por n que poseen un determinante equivalente a la cifra 1, con las entradas en el cuerpo C de los complejos y también con el cáluclo de la agrupación que se da a partir de el producto de matrices. Es denotado como SU(n). Este es un subgrupo del grupo unitario U(n) siendo también un subgrupo del grupo general lineal GL(n, C). Vamos a asumir entonces que n ≥ 2
Forma de las matrices
Hay un cumplimiento de las normas de conmutación del álgebra de Lie SU(2):
![]()
La forma de símbolo de Levi-Civita, también es denominado símbolo de permutación y puede ser definido de la siguiente forma,

Así mismo las matrices cumplen con la regla anticonmutativa,
![]()
Otras propiedades importantes son las siguientes:
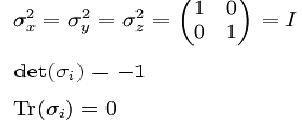
Veamos ahora diferentes casos.
espín 1/2
Existen tres matrices de Pauli, tal como en las dimensiones del álgebra del Lie del grupo SU(2). Su forma lineal mas habitual es la que vemos a continuación:
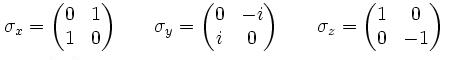
espín 1
Se suele llamar matrices de Pauli a diferentes formas de representación lineal que difieren a las que fueron utilizadas en el caso de espín 1/2 que se vio anteriormente. Por ejemplo para hacer una representación del espín de una partícula que tiene como valor numérico 1, se utilizará la representación lineal a partir de matrices de 3×3:
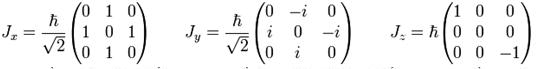
espín 3/2
Correlativamente al caso anterior para espín 3/2 usualemte es utilizada la representación siguiente: