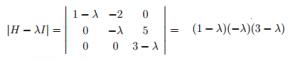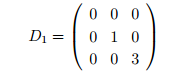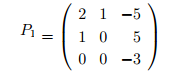Diagonalización de matrices

Como ya sabemos mucho sobre matrices, vamos a indagar un poco más estudiando la diagonalización de nuestras queridas amigas las matrices. Este concepto se estudio en los primeros cursos universitarios tanto de ingenierías como en el grado de Economía o Empresariales.

Diagonalizar como su nombre indica es un proceso mediante el cual obtenemos una matriz diagonal de nuestra matriz original, y por tanto facilitará la realización de algunos cálculos. Antes de indicar los pasos que tenemos que llevar a cabo, daremos unos concepto previos:

CONCEPTOS PREVIOS

Definición: Dado un vector no nulo x=(x1,x2,….,xn) diremos que es un vector propio o un autovector de la matriz A, si existe un escalar λ tal que: Ax= λx. Al valor del escalar λ se le denomina valor propio o autovalor de la matriz A.

Observación: Todo vector propio tiene asociado un único valor propio.

Propiedad: Se x1,x2,x3…xk son vectores propios de la matriz A cuyos valores propios correspondientes son λ1, λ2,…. λk, todos ellos distintos; entonces los vectores son linealmente independientes.

Definición: Llamamos polinomio característico asociado a la matriz A, al polinomio que resulta al desarrollar el siguiente determinante: |A- λI|, donde I es la matriz identidad del orden correspondiente (en este caso, el mismo orden que A para que puedan restarse).

Igualando el polinomio característico a 0, |A- λI|=0, obtenemos la ecuación característica.

Propiedad: Los valores propios de la matriz A serán las soluciones del polinomio característico.

DIAGONALIZACIÓN DE MATRICES

Definición: Diremos que una matriz A es diagonalizable si podemos encontrar una matriz invertible P y una matriz diagonal tal que:

A la matriz P se la denomina matriz de paso. Además cuando se da esta situación diremos que A y D son semejantes.

Propiedad: Los elemento que forman la matriz diagonal coinciden con sus valores propios.

Propiedad: Si una matriz A tiene todos sus valores propios distintos, entonces A es diagonalizable. En el caso en el que alguno de sus valores propios tenga una multiplicidad distinta de 1, solo será diagonalizable cuando la multiplicidad coincida con la dimensión del espacio vectorial asociado.

Pasos para diagonalizar una matriz:

Diagonalizar si es posible la matriz H: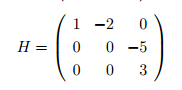

1º) Calculamos la ecuación característica para obtener los valores propios: | H- λI|=0

Por tanto, los valores propios que obtenemos son: λ1=0, λ2=1, λ3=3.

2º) Como todos los valores propios son distintos, entonces podemos admitir que nuestra matriz A es diagonalizable. La matriz D diagonal será:

Observación: El orden en el que coloquemos los valores propios en la diagonal es indiferente, pero tendremos que tener cuidado a la hora de calcular la matriz de paso, P (ya que cada vector propio irá en la columna correspondiente a su valor propio).

3º) Una vez que ya tenemos los valores propios, vamos a calcular la matriz de paso P, para ello, buscamos una base para cada uno de los subespacios vectoriales:

-Si λ=0, entonces calculamos (H-0 λ), para calcular el núcleo, escribimos el sistema que resulta cuando hacemos (H-0 λ)X=0, donde X es el vector columna formado por X=(x y z)´.

Obtenemos la base {(2,1,0)}

-Análogamente,si λ=1, entonces calculamos (H-1 λ) y calculamos su núcleo:

Obtenemos la base {(1,0,0)}

-Por último, cuando λ=3, entonces calculamos (H-3 λ) y calculamos su núcleo:

Obtenemos la bse {(-5,5,-3)}

Por tanto la matriz de cambio P será:

Si queremos comprobar que está bien hecho, siempre podemos hacer la inversa de P y comprobar que al realizar el producto de P por D, y este a su vez por la inversa, obtenemos la matriz inicial, H.