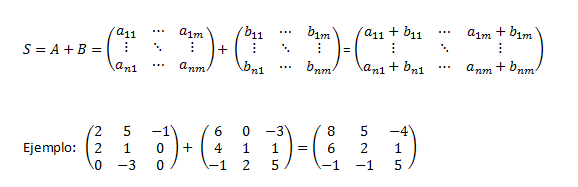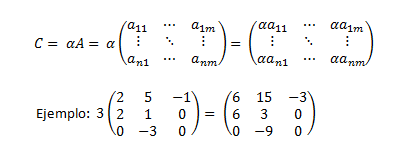Operaciones con matrices

Después de haber visto los tipos de matrices que nos podemos encontrar, estamos preparados para introducir las operaciones. Comenzaremos viendo la suma de matrices y el producto de un escalar por una matriz que dotarán al conjunto de las matrices de una estructura de espacio vectorial sobre un cuerpo K. Y para finalizar, veremos el producto de matrices.

SUMA DE MATRICES:

Se define la matriz suma de A y B como una nueva matriz S en la que cada uno de sus elementos está formado por la suma del elemento correspondiente de A con el de B, es decir, sij=aij+bij. Para poder sumar dos matrices es necesario que las dos tengan el mismo orden, que por tanto, coincidirá con el orden de la matriz resultante.

Como podemos observar en el ejemplo, los elementos de la matriz se suman utilizando las propiedades de los números enteros. Por tanto, podemos definir la resta de dos matrices A y B, como la suma de la matriz A con la opuesta de B: A- B = A + (-B)

Propiedades de la suma de matrices:

1. Es asociativa: A+(B+C)=(A+B)+C

2. Tiene elemento neutro, es decir, existe una matriz que al sumarla con A se obtiene A, que es la matriz nula. A + 0 =A

3. Tiene elemento simétrico, es decir, existe una matriz que al sumarla con A se obtiene el elemento neutro (la matriz nula), que es la matriz opuesta de A: A + (-A) = 0

4. Es conmutativa: A+ B = B+A

PRODUCTO DE UN ESCALAR POR UNA MATRIZ

Se define el producto de un escalar (α ∈K) por una matriz (A) , como una nueva matriz C en la que cada elemento de A queda multiplicado por α, es decir, cij= αaij.

Propiedades del producto de un escalar por una matriz:

1. Se cumple la propiedad distributiva respecto de la suma de matrices:

α(A+B)= αA+αB

2. Es distributiva respecto la suma de escalares: (α+µ)A=αA+µA

3. Pseudoasociativa: (α∙µ)A= α(µA), donde • indica el producto entre escalares.

4. Neutralidad del 1: 1•A=A•1=A

Por tanto podemos decir, como ya habíamos aventurado al principio, que el conjunto de las matrices de orden nxm tiene estructura de espacio vectorial sobre el cuerpo K.

PRODUCTO DE MATRICES

En primer lugar, para poder definir el producto de dos matrices, debemos tener en cuenta que sólo se podrán multiplicar cuando el número de columnas de la primera matriz (nxm) coincida con el número de filas de la segunda matriz (mxl). Y que la matriz resultante, tendrá el número de filas de la primera matriz, y el número de columnas de la segunda (nxl)

Teniendo en cuenta estas condiciones, se define la matriz producto de A y B como una nueva matriz C en la que sus elementos se obtienen al sumar los productos obtenidos de multiplicar los elementos correspondientes de la fila de A con los de la columna de correspondiente de B: cij= ai1b1j+ai2b2j+…….+aimbmj.

Propiedades de la multiplicación de matrices:

1. Es asociativa: A(BC)=(AB)C

2. No es conmutativa.

3. Tiene elemento neutro, que es la matriz identidad, y que depende del lado por el que se multiplique:

4. Se cumple la propiedad distributiva respecto a la suma de matrices: A(B+C)=AB+AC