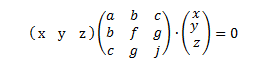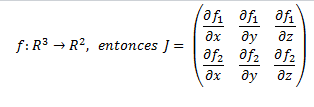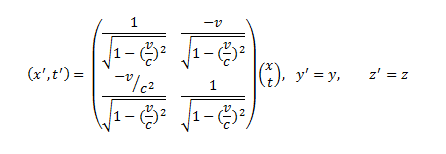Aplicaciones de las matrices

Una vez que ya conocemos a fondo las matrices, puesto que hemos visto los distintos tipos que hay y las operaciones que podemos realizar con ellas. Vamos a ver sus aplicaciones, ya que las matrices son una herramienta muy útil no sólo en el campo de las matemáticas y la física como era de esperar; sino también en el campo de las ciencias sociales, por ejemplo en economía y en geografía. Esta gran utilidad se debe a que las matrices aportan un nuevo lenguaje facilitando el trabajo en una gran cantidad de ámbitos.

Empezaremos en primer lugar con las aplicaciones en Matemáticas, donde vamos a distinguir las aplicaciones en las distintas ramas:

Álgebra lineal:

1. En esta rama destaca la utilidad en la resolución de sistemas de ecuaciones de la forma AX = B, mediante el cálculo de la matriz inversa:

2. Estudio de las aplicaciones lineales entre dos espacios vectoriales mediante la matriz asociada, que nos permite calcular el núcleo y la imagen.

Geometría:

1. Para expresar la ecuación de un giro de ángulo α alrededor del eje OZ:

2. Para representar las ecuaciones de las formas cuadráticas. Haciendo el estudio de la matriz correspondiente podemos clasificar la cuadrática en definida positiva, semidefinida positiva, definida negativa o semidefinida negativa. La matriz asociada a la forma cuadrática siempre es una matriz simétrica.

Análisis:

En la rama del análisis se utilizan las matrices jacobianas, que se usan para expresar las derivadas parciales de una función en varias variables:

Si f(x,y,z) está definida de la siguiente forma:

Continuamos con las aplicaciones en la Física. La aplicación más importante en este campo son las transformaciones de Lorenz, que dan las ecuaciones del movimiento de un punto en línea recta y sobre el plano conocida la velocidad de la luz.

Por ejemplo: suponiendo que el punto se desplaza sobre el eje OX y que estamos en un espacio tetradimensional, donde la cuarta dimensión es el tiempo, entonces, el punto tendrá como coordenadas inciales (x,y,z,t) y como finales (x’,y’,z’,t’). Las ecuaciones que dan esta transformación son:

Donde c representa la velocidad de la luz.

Una vez que ya hemos visto algunas de las aplicaciones más importantes en Ciencias, vamos a ver la importancia que tienen en las Ciencias Sociales. Empezaremos primero con la Economía.

Las matrices se utilizan para la presentación de datos de un problema en forma de tabla de doble entrada. Un ejemplo de esto es el modelo Input-Output, que permite solucionar problemas macroeconómicos, algunos de los cuáles son:

– Orientar o estructurar los sectores productivos.

– Poder predecir las demandas de producción.

– Interpretar las relaciones económicas existentes entre los distintos sectores de producción.

Si continuamos por la Geografía, también aparecen cuando hay tablas de doble entrada, por ejemplo, para hacer referencia a la distancia que hay entre varias ciudades:

Y hasta aquí algunas de las aplicaciones más importantes de nuestras amigas las matrices, ya que las hemos conocido mucho más a fondo, estudiando los diferentes tipos, las operaciones que podemos realizar y finalmente las múltiples aplicaciones en los diversos campos de nuestra vida…