Mapa de Karnaugh

El mapa de Karnaugh o diagrama de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como K-Mapa o KV-Mapa) fue inventado en 1950 por Maurice Karnaugh, físico y matemático de los laboratorios Bell. Este es un tema de gran extensión, por lo cual en este artículo veremos tan solo algunas partes básicas.

El mapa de Karnaugh es uno de los métodos utilizados para la minimización de funciones algebraicas booleanas y es utilizado también para minimizar expresiones del tipo suma de productos o productos de sumas, obteniendo así otra suma de productos y otros productos de sumas. La expresión obtenida será mínima.

Se trata de una serie de cuadrados, cada cuadrado constituye una línea de la tabla de verdad. Dicha tabla despliega el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se puedan establecer a sus componentes. Como la tabla de verdad de una función de N variables tiene 2N filas, el mapa K correspondiente debe poseer 2N cuadrados. Cada cuadrado tiene como componente un 0 ó un 1, esto depende del valor que toma la función en cada fila. Las tablas de Karnaugh pueden ser utilizadas para funciones de hasta 6 variables.

los Mapas de Karnaugh sirven para obtener una función mínima de dos niveles Suma de Productos. Una expresión de dos niveles es considerada, expresión mínima si:

1. No hay otra expresión equivalente que contenga menos productos.

2. No hay otra expresión equivalente que conste con el mismo número de productos, con un menor número de literales.

Es importante observar si hablamos de UNA expresión mínima y LA expresión mínima, ya que pueden existir varias expresiones distintas, pero equivalentes, que satisfagan esta definición y posean igual número de productos y literales.

La minimización de funciones sobre el mapa de Karnaugh, aprovecha que las casillas están dispuestas de tal forma que entre una casilla y otra, en forma horizontal o vertical existe adyacencia lógica. O sea que entre una casilla y otra solo cambia una variable.

Definimos los mintérminos adyacentes, como dos mintérminos que difieren en una variable. Agrupando casillas adyacentes adquirimos términos productos que descartan las variables complementadas, resultando una versión facilitada de la expresión.

Se procede agrupando «unos» adyacentes en el mapa. Cada grupo corresponderá a un término producto, y la expresión final dará un OR (suma) de todos los términos producto. Buscamos obtener el menor número de términos productos posible. Esto implica que cada termino producto debe contener el mayor numero de mintérminos posibles.

Veamos ahora un mapa de Karnaugh, resultado de la siguiente función:

Es importante saber que:

La función está expresada en forma canónica, por lo cual cada mintérmino «colocará» un 1 en su casilla correspondiente como se muestra en el mapa:

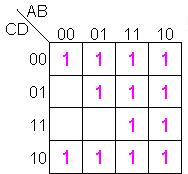
Supongamos por un momento que agrupemos los «unos» del mapa de Karnaugh como se muestra en la siguiente figura:

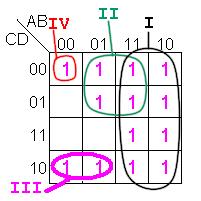
Según esto tendríamos cuatro términos:

Observemos que cuando agrupamos mayor cantidad de «unos», el término va teniendo menos literales. El agrupamiento se hace con una cantidad de «unos» que son potencias de 2. De esta forma agrupamos 2 mintérminos, 4 mintérminos y 8 mintérminos. Cada vez que aumentamos, el término descarta una variable. En una función de 4 variables, un término que posea un solo «uno» tendrá las cuatro variables. Es un término canónico. Si agrupamos dos mintérminos eliminaremos una variable y el término resultará de tres variables. Si agrupamos cuatro «unos» eliminaremos dos variable quedando un termino de dos variables y si agrupamos ocho «unos» se eliminaran tres variable para quedar un termino de una variable. Esto es producto de la adyacencia entre casillas, cada vez que agrupamos, se eliminan las variables que se complementan.

En el ejemplo anterior la función obtenida es:
_ _ _ _ _ _ _
f = A B C D + A C D + B C + A

Pero, aún no sabemos si es la expresión mínima .Observemos la siguiente figura:

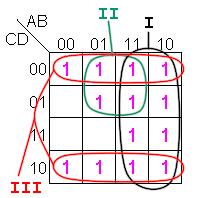
La forma de agrupar nos da como resultado:

Es de gran importancia que al «tomar» un uno, se agrupe con todos los unos adyacentes, aún si estos uno forman parte de otros grupos.

Para simplificar funciones utilizando mapas de Karnaugh, tengamos en cuenta lo siguiente:

• Cada casilla (mintérmino) en un mapa de Karnaugh de n variable posee n casillas adyacentes, por lo cual cada par de casillas defiere en una variable

• Si se combinan las casillas en un mapa de Karnaugh,se agrupa un número de mintérminos, siendo potencia de dos. Agrupando dos casillas eliminamos una variable, agrupando cuatro casillas eliminamos dos variables, y así sucesivamente. Debemos agrupar tantas casillas como sea posible; cuanto mayor sea el grupo, el termino producto resultante tendrá menos literales. Es importante incluir todos los «unos» adyacentes a un mintérmino que sea igual a uno.

• Para que hayan menos términos en la función simplificada, tenemos que formar el menor número de grupos posibles que cubran todas las casillas (mintérminos) que sean iguales a uno. Un «uno» puede ser utilizado por varios grupos. Si un grupo se incluye completamente en otro grupo, o sus «unos» están cubiertos por otros grupos, no hará falta incluirlo como termino.