Leonhard Euler

En nuestro recorrido por los conocimientos matemáticos, merece que de vez en cuando hagamos una pequeña pausa en el camino, para ir conociendo a los personajes de esta obra, gracias a los cuáles podemos tener conocimiento de diversas causas.

Hoy nos vamos a centrar en Leonhard Euler, famoso matemático y físico suizo del siglo XVIII que además también destacó en el aspecto político de su época. Nació en Basilea (Suiza), aunque su vida se desarrolla principalmente entre Rusia y Alemania.

A continuación vamos a conocer cuáles fueron algunas de sus aportaciones a las matemáticas en la mayoría de sus áreas: geométrica, trigonometría, álgebra, teoría de números, cálculo, además de la notación matemática. También realizó importantes trabajos en física, como por ejemplo su estudio sobre la teoría lunar.

-Notación matemática: Euler introdujo el concepto de función, así como la notación que utilizamos hoy en día: f(x). También le debemos a él, la notación de las funciones trigonométrica, y la notación del número trascendente e; y la i para referirnos a la unidad imaginaría (la raíz de menos uno). Podemos añadir, que colaboró en la difusión del número pi, el cuál nos da el valor del cociente entre la longitud de una circunferencia y la de su diámetro, aunque no fue el primero que la usó. Además estos últimos números, se ponen de manifiesto en la identidad que lleva su nombre: la identidad de Euler: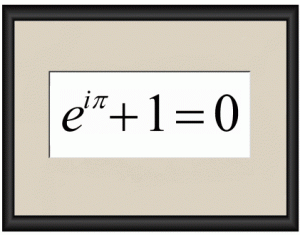

-Análisis matemático: Es conocido por usar frecuentemente series de potencias. De hecho uno de sus logros más famosos fue el del desarrollo de la función arcotangente por series de potencias. Introduce el uso tanto de la función exponencial como de los logaritmos en las demostraciones.

-Álgebra: Todos conocemos la fórmula que hay que utilizar para resolver ecuaciones de segundo grado, la cual se debe a Diofanto. En cambio, Euler desarrolló un método para resolver ecuaciones de cuarto grado. Además, debido al avance que realizó en el análisis complejo, también nos dejó otras ecuaciones conocidas como ecuaciones de Euler-Lagrange.

-Teoría de Números: Euler une dos ramas separadas de las matemáticas, métodos analíticos con problemas teóricos de carácter numérico, para crear un nuevo campo: la teoría analítica de números. En este campo destaca por haber unido la naturaleza de los números primos con sus conocimientos de análisis matemático, demostrando de esta manera que la suma de los inversos de los números primos es divergente. También demostró algunos enunciados que todavía no habían sido demostrados, como el pequeño Teorema de Fermat y las identidades de Newton.

-Teoría de grafos : Dentro de la teoría de grafos, fue capaz de resolver el famoso problema de los puentes de Königsberg diciendo que no tenía solución; lo cual supuso el primer teorema de la teoría de grafos.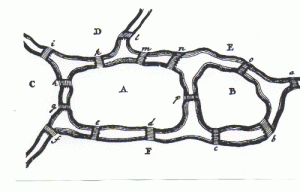

-Geometría: Por último en el campo de la geometría, le debemos el descubrimiento de que los tres puntos notables de un triángulo: baricentro, circuncentro y ortocentro; todos ellos están sometidos a la ecuación de una única recta, denominada la recta de Euler, como podemos observar en la siguiente imagen.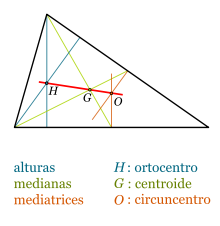

CURIOSIDADADES

Para finalizar, veremos un par de curiosidades que hacen referencia a nuestro personaje de hoy:

-En primer lugar, se dice que fue él quien dio origen al conocido pasatiempo al que todos hemos jugado alguna vez: el Soduko; a través de unas pautas en el cálculo de probabilidades.

-Y por último, resaltando así su importancia en nuestra historia, la imagen de Euler aparecen en una edición de billetes de 10 francos suizos. Pero no sólo en billetes, sino también en sellos tanto alemanes como rusos y suizos, los países por los que pasó.