Fórmula de De Moivre
La fórmula de De Moivre se denomina de esta forma debido al matemático francés Abraham de Moivre, quien afirma que para cualquier número real, para cualquier número complejo y también para cualquier entero n, se verifica lo siguiente:
![]()
La expresión «cos x + i sen x» a veces es abreviada como cis x.
Esta fórmula es de suma importancia ya que conecta a los números complejos con la trigonometría. Al expandir la parte izquierda de la igualdad y si comparamos la parte real con la imaginaria, es posible que se procedan expresiones de gran utilidad para cos(nx) y sen(nx) en términos de cos(x) y sen(x). Esta fórmula puede también ser utilizada para hallar expresiones claras y explicitas para la enésima raíz de la unidad, eso es, números complejos z tal que zn = 1.
Abraham De Moivre fue gran amigo de Isaac Newton; en 1698 Newton escribió que ya conocía dicha fórmula desde 1676.
Hoy se suele demostrar la fórmula de De Moivre con el uso de la fórmula de Euler, esta última formula se denomina así por el matemático y físico ruso Leonard Euler; sin embargo, cronológicamente no fue de esta forma.
Euler conocía muy bien lo siguiente:
![]()
De Moivre la escribió antes de final del XVII. De dicha fórmula fue donde Euler logró obtener una fórmula para el coseno:
![]()
y otra para el seno
![]()
A continuación tomó θ como infinitesimal y n como infinitamente grande. Concluyó en que las relaciones entre θ y n son tales que su producto es finito, θn→ν, y agregando lo siguiente:
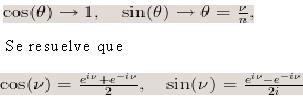
Podemos concluir en que La fórmula de Moivre permite obtener de forma simple, fórmulas trigonométricas que expresan el seno y el coseno de un ángulo múltiple en función del seno y coseno del ángulo simple.
Además de su relevancia en la trigonometría, la fórmula de De Moivre también tiene aplicaciones en otras áreas de las matemáticas. Por ejemplo, es fundamental en el estudio de las series de Fourier, que son una herramienta esencial en el análisis de señales y sistemas. Las series de Fourier permiten descomponer una función periódica en una suma de senos y cosenos, lo que facilita su análisis y manipulación.
La fórmula de De Moivre también es útil en el cálculo de raíces de números complejos. Esto es especialmente relevante en la resolución de ecuaciones polinómicas, donde las raíces pueden ser reales o complejas. La fórmula permite expresar las raíces de un número complejo en una forma fácilmente manejable, lo que simplifica enormemente el proceso de resolución de la ecuación.
En el campo de la física, la fórmula de De Moivre es utilizada en la descripción de fenómenos ondulatorios, como las ondas de luz o sonido. En estos contextos, las cantidades de interés suelen ser oscilantes, y la fórmula de De Moivre proporciona una forma conveniente de trabajar con ellas.
En resumen, aunque la fórmula de De Moivre puede parecer abstracta y alejada de la realidad, en realidad es una herramienta matemática extremadamente útil con una amplia gama de aplicaciones en diversas disciplinas. Su estudio y comprensión son fundamentales para cualquier persona que desee profundizar en el fascinante mundo de las matemáticas.
