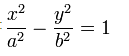Las cónicas
Las cónicas son las figuras geométricas que aparecen cuando hacemos la intersección de un cono con un plano. Como podemos ver en la siguiente imagen, según el ángulo de inclinación del plano, que denotamos por ß, podemos encontrarnos con las siguientes figuras: una circunferencia, una elipse, una parábola o una hipérbola, de mayor a menor inclinación.
Estudiemos a continuación una a una las características más importantes de cada una de las cónicas.
CIRCUNFERENCIA
Aunque es la primera que nos encontramos en las intersecciones de nuestro cono, es un caso particular de la elipse. La circunferencia es el resultado de la intersección de un plano de forma perpendicular al eje. Por tanto el ángulo de inclinación ß= 90º.
Definición formal: Denominamos circunferencia al conjunto de los puntos del plano que equidistan de un punto fijo, llamado centro.
ELIPSE
La elipse surge al realizar la intersección de una superficie cónica con un plano oblicuo al eje, es decir, un plano que no sea paralelo ala generatriz del cono. Por tanto el ángulo de inclinación oscilará entre: 0<ß<90º.
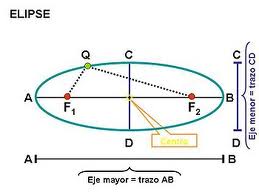
Definición formal: Llamamos elipse al conjunto de los puntos del plano tales que si sumamos las distancias a dos puntos fijos, denominados focos F1 y F2, ésta es constante. Otros elementos representativos de una elipse que utilizamos para su descripción son el centro O, el eje mayor AB, el eje menor CD, y la distancia focal, OF.
La ecuación de la elipse que tiene por centro el punto (0,0) es: 
PARÁBOLA
La parábola se obtiene a partir de la intersección de una superficie cónica y un plano oblicuo al eje que sea paralelo a la generatriz. Por tanto el ángulo de inclinación coincide con el ángulo de conocidad. Tanto la parábola como la hipérbola son curvas abiertas cuyo trazo continua hasta el infinito.
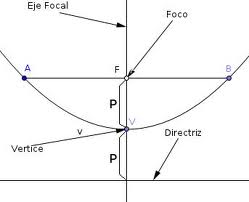
Definición formal: Una parábola es el conjunto de puntos de un plano que equidistan de un punto fijo, conocido como foco, y de una recta, llamada directriz.
Los elementos característicos de una parábola son: su eje o eje de simetría, el vértice (que corresponde con el máximo o mínimo de la parábola según sea su curvatura).
La ecuación de una parábola cuyo vértice es el (0,0) y su eje el eje de ordenadas es:
HIPÉRBOLA
Por último, la hipérbola se obtiene al realizar la intersección de una superficie cónica y un plano oblicuo al eje, pero en este caso, el ángulo de inclinación tiene que ser más pequeño que el que forman el eje y la generatriz. Como ya hemos dicho en el caso anterior, también es una curva abierta. La hipérbola consta de dos ramas separadas, de tal forma que tiene dos asíntotas.
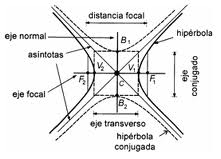
Definición formal: Denominamos hipérbola al conjunto de los puntos del plano tales que si realizamos la diferencia de las distancias a dos puntos fijo, denominados focos, esta es constante y además, menor que la distancia entre los focos.
Los elementos representativos de una hipérbola son: el centro, O; los vértices, así como la distancia entre los vértices y la distancia entre los focos.
La ecuación de una hipérbola que tiene por centro el (0,0) es: