Coordenadas polares

Normalmente estamos acostumbrados a trabajar en el sistema cartesiano, donde un punto viene determinado por dos coordenadas (x,y), cuyos valores indican la distancia al origen (el punto de intersección donde se cortan los dos ejes) en cada uno de los ejes.

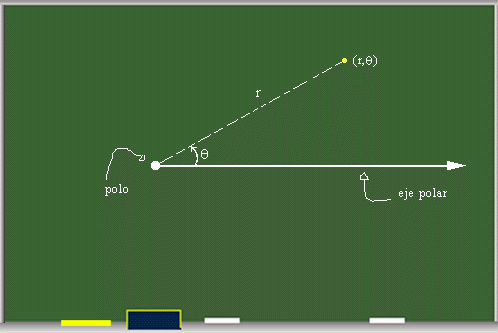
No obstante, para poder representar puntos en el plano también podemos utilizar otros sistemas, como el que vamos a estudiar hoy, el sistema de coordenadas polares, donde los puntos vienen determinados por un ángulo (θ) y una distancia (r). Como podemos ver en la siguiente imagen, para medir nuestro ángulo en radianes, se necesita una semirrecta a la que dotamos de dirección, esta recta se denomina eje polar, donde 0 ≤ θ ≤ 2 π. Por otro lado, para medir la distancia, nos valemos de un punto fijo denominado polo.

PUNTOS EN COORDENADAS POLARES

Por tanto, un punto en este caso queda determinado por el par (r, θ). Cuando necesitamos situar un punto en coordenadas polares tenemos que realizar los siguientes pasos:

1º. Trazar una circunferencia de radio r.

2º. Trazamos una recta con ángulo de inclinación θ, cuyo vértice se centrará en el centro de la circunferencia, este es nuestro polo.

3º. Nuestro punto será el punto de intersección entre la circunferencia y la recta.

Ejemplo: Situar los siguientes puntos: (1, π), (3, π/4), (3, π/6), (2, 3π/2) y (3, 7π/4).

Observación: Los puntos en el sistema de coordenadas polares no tienen una expresión única, sino que pueden representarse con un número infinito de coordenadas diferentes. Este hecho no se da cuando trabajamos con coordenadas cartesianas. La inexistencia de correspondencia biunívoca es debida a dos circunstancias:

1. Cuando definimos un punto por medio de un ángulo y una distancia, ese punto coincide con el indicado por ese ángulo más un número de revoluciones completas y la misma distancia. Es decir el punto (r, θ) es el mismo punto que cualquiera que se pueda expresar como (r, θ ± n∙2π ), donde n es cualquier número entero. Por ejemplo, el punto (1, π) es el mismo que el (1, 3π) ya que el ángulo que determinan es el mismo.

2. La definición del centro de coordenadas viene dada por una distancia nula que es independiente de los ángulos dados. Por regla general utilizamos (0, θ) para representar el polo.

CAMBIO A COORDENADAS POLARES

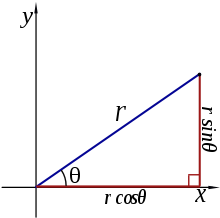
En algunas ocasiones, es más conveniente o más fácil trabajar con coordenadas polares en lugar de con cartesianas, como puede ser en la resolución de algunas integrales dobles. Por tanto, es necesario que pasemos de coordenadas cartesianas a polares. Para ello definimos un sistema de coordenadas polares sobre el plano XY, tomando como centro de coordenadas el origen (0,0), de tal forma que las coordenadas de un punto P quedan definidas por la distancia del punto al origen y el ángulo que forma el vector posición con el eje 0X, tal y como podemos ver en la siguiente imagen.

Como podemos observar, utilizando nuestro conocimientos de las razones trigonométricas tenemos que: x=r∙cos θ e y = r∙sen θ.